Etude Données Hospitalières Covid-19 – I

Cette étude observationnelle porte sur les données hospitalières fournies par Santé Publique France relatives au Covid-19 du 18 mars au 20 mai 2020.

Nous nous sommes intéressés au Taux de décès par rapport aux hospitalisations cumulées en France par département et par région. Ceci pourrait être intéressant pour évaluer une efficacité hospitalière.

L’étude porte sur 99114 hospitalisations et 17837 décès.

Les données originales ont été récupérées respectivement sur la page « Données hospitalières relatives à l’épidémie de COVID-19 » pour le fichier « donnees-hospitalieres-covid19-2020-05-21-19h00.csv » et sur la page « Données des urgences hospitalières et de SOS médecins relatives à l’épidémie de COVID-19 » pour le fichier « sursaud-covid19-quotidien-2020-05-21-19h00.xlsx » et du site data.gouv.fr.

Toutefois les données disponibles changeant tous les jours sur le site de Data.gouv.fr , vous pouvez récupérer les données du 21 mai et tous les autres fichiers nécessaires gratuitement dans notre boutique à l’adresse https://www.anakeyn.com/boutique/produit/donnees-etude-covid19-au-21-05-20/

Dans cette étude nous avons utilisé les outils Excel, Dataiku et R pour agréger et traiter les données.

Limite des données fournies

Sur les pages respectives de data.gouv.fr des descriptions des jeux de données sont fournies.

Le fichier « donnees-hospitalieres-covid19-2020-05-21-19h00.csv » fournit des données relatives aux nombres de personnes hospitalisées au jour J. Il donne aussi des informations de décès (le cumul des décès depuis le début de l’épidémie) et de sexe mais pas de classes d’âge.

Le fichier « sursaud-covid19-quotidien-2020-05-21-19h00.xlsx » fournit des informations sur les entrées en hospitalisation pour motif de Covid19, des données de sexe et de classes d’âge mais pas d’information sur les décès du jour.

Il existe aussi des incohérences dans les données qui sont décrites dans les rubriques « Anomalies détectées dans les fichiers » sur les pages respectives de data.gouv.fr

En conséquence, nous allons nous attacher à déterminer le taux de décès cumulés vs les hospitalisations cumulées au jour J. Les autres indicateurs devront aussi évoluer dans le temps proportionnellement aux cumuls des variables.

Préparation des Données avec Excel

Fichier des urgences

Dans un premier temps nous avons transformé le fichier « sursaud-covid19-quotidien-2020-05-21-19h00.xlsx » pour ne garder que les informations d’hospitalisations, les regrouper sur une ligne par jour et par département et de calculer les cumuls des variables pour obtenir le fichier « covid19-2020-05-20-02-24-Urg-Cumul.xlsx« .

Notez que nous avons des données depuis le 24/02/2020, avant le début des premiers cas, ce qui nous permet de connaitre les entrées en hospitalisation depuis le début de l’épidémie.

Nous avons ensuite calculé les proportions pour chaque variable cumulée au jour J dans le fichier : « covid19-2020-05-20-02-24-Urg-Cumul-Prop.xlsx« 

Fichier des hospitalisations

Avec le fichier « donnees-hospitalieres-covid19-2020-05-21-19h00.csv« , nous avons fait la même opération, à savoir regrouper les informations sur une ligne par jour et par département et calculer les cumuls pour donner le fichier « covid19-2020-05-20-03-18-Global-Cumul.xlsx« 

Nous avons ensuite calculé les proportions corerspondantes à chaque jour : « covid19-2020-05-20-03-18-Global-Cumul-Prop.xlsx« 

Regroupement des deux fichiers :

Attention : Avant de faire le regroupement vérifiez que vous avez enlevé les formules des fichiers (faire un copier/coller valeurs dans Excel) afin d’éviter des erreurs.

Nous avons ensuite « Copié/collé » les données du fichier « Global » : « covid19-2020-05-20-03-18-Global-Cumul-Prop.xlsx » dans le fichier « Urgences » « covid19-2020-05-20-02-24-Urg-Cumul-Prop.xlsx« .

Si vous souhaitez faire l’opération attention à bien cadrer les jours (démarrer au 18/03/20) et les départements. Enlevez ensuite le département 972 qui n’a pas de données d’urgences et notamment de classe d’âge.

Vous obtenez le fichier : « covid19-2020-05-20-03-18-Urg-Cumul-Prop-Global-Cumul-Prop.xlsx« 

Voilà votre fichier est prêt (il est aussi disponible dans liste de nos fichiers) , on va pouvoir l’utiliser dans Dataiku.

Traitement du fichier de données avec Dataiku

Pour installer Dataiku reportez vous à notre article Installation et prise en main de Dataiku DSS 6.0 sous Windows 10.

Rappel : pour démarrer Dataiku DSS dans la console Ubuntu :

DATA_DIR/bin/dss start

Puis ensuite ouvrez un navigateur Chrome ou Firefox et allez à l’adresse : http://<your server address>:11000. Souvent (et pour moi) http://127.0.0.1:11000.

Dans Dataiku, créez un nouveau projet et importer le fichier covid19-2020-05-20-03-18-Urg-Prop-Global-Cumul-Prop.xlsx.

Utilisez pour cela la fonction « Import New Dataset » et ensuite choisir l’option « Files ».

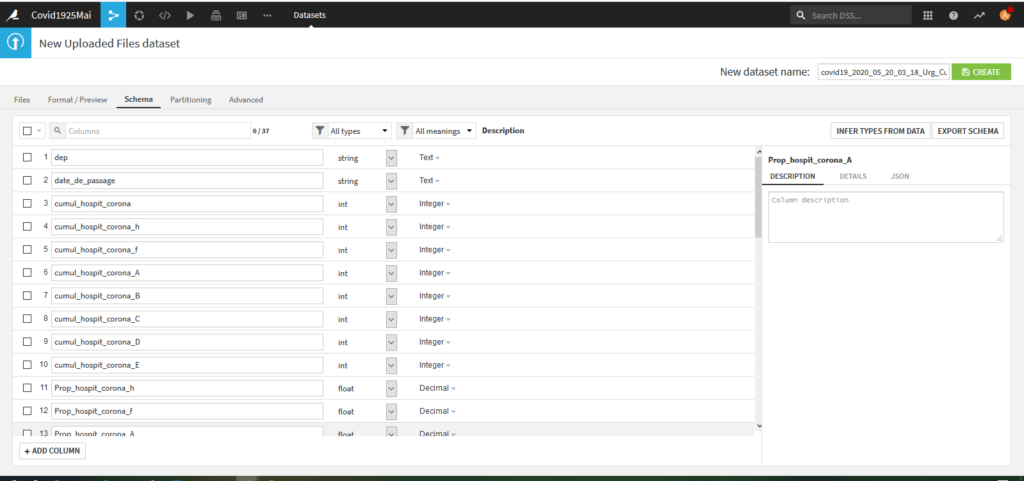
Lors de la prévisualisation de l’import, allez dans l’onglet « schema » pour spécifier les types des variables importées :

• Pour dep et jour : string/Text
• pour les variables entières : int/Integer
• pour les variables décimales (les ratios) : float/Decimal

L’importation nous crée un jeu de données nommé « covid19_2020_05_20_03-18-Urg_Prop_Global_Cumul_Prop_global« .

On va ensuite « parser » la variable « date_de_passage » en date. pour cela on va utiliser une recette (recipe) « prepare » accessible quand on retourne sur le « flow » :

Profitons-en pour donner un nom plus court au jeu de données par exemple « covid19« 

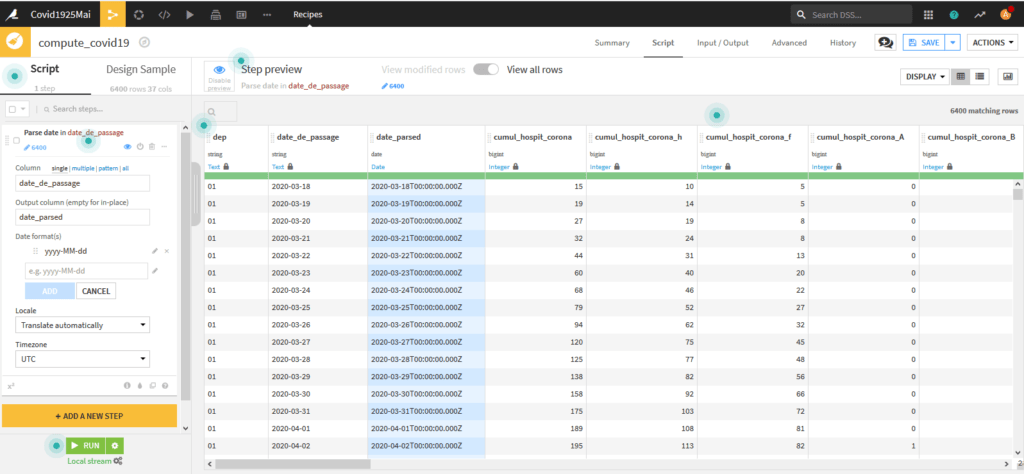
Dans la recette « prepare » ajoutez une étape « Add a new step » et choisissez dans la liste des outils pour Date : « Parse to standard Date Format ». Créez la variable « date_parsed » à partir de « date_de_passage« , notez que le format de date en entrée est yyyy-MM-dd (année-mois-jour).

Quand vous cliquez sur Add au niveau du format la nouvelle variable apparait dans la prévisualisation :

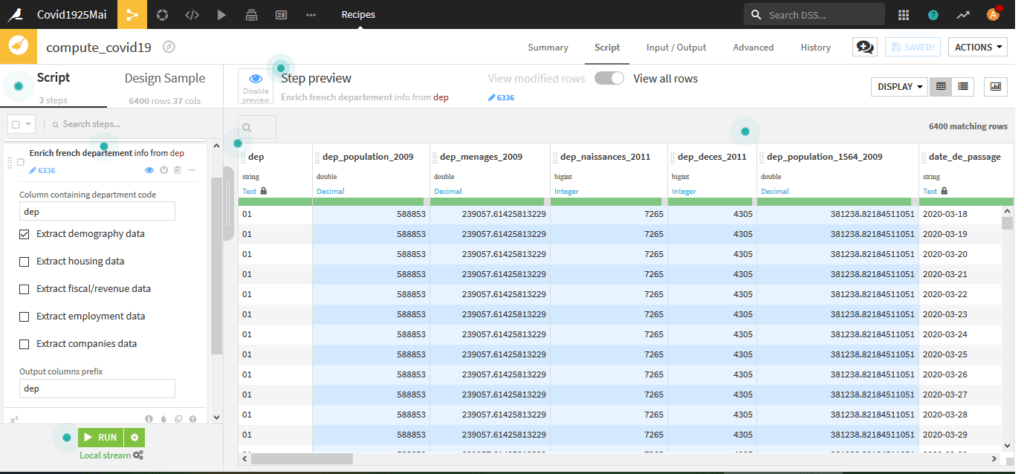
Nous allons aussi ajouter des données démographiques par département, cliquez à nouveau sur « Add A New Step » puis choisissez « Enrich » et « Enrich from French department« 

Rem : la population pour Mayotte n’est pas disponible, on l’indiquera à la main dans Excel Plus tard. (270 372 habitants).

Cette information nous servira plus tard pour calculer des facteurs pour 100000 habitants.

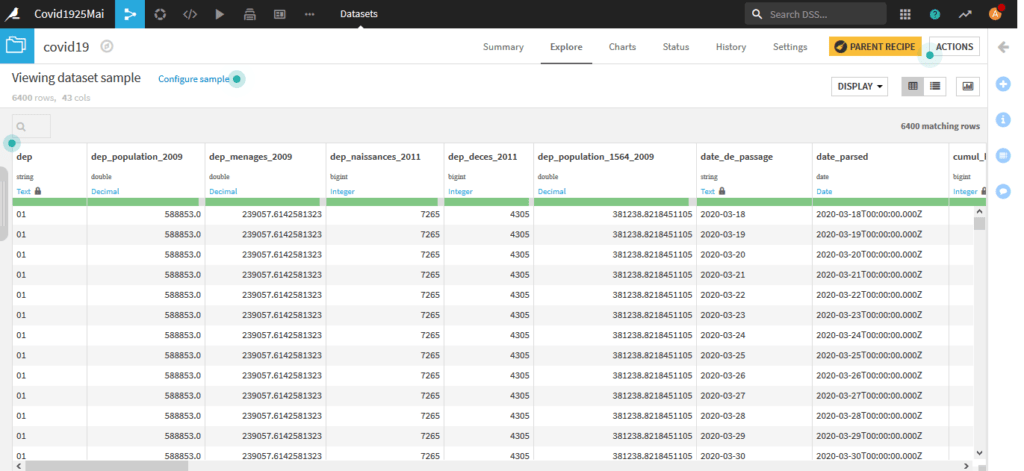
Cliquez ensuite sur Run pour créer le nouveau jeu de données appelé « covid19« . Une fois le job effectué ouvrez le lien « explore dataset covid19 » en bas pour voir les données :

Evolution des hospitalisations et réanimations en France du 19 mars au 20 mai 2020.

On va créer notre premier graphique, sur le menu horizontal en haut cliquez sur Charts. Vous avez un outil de création de graphique un peu comme dans Tableau.

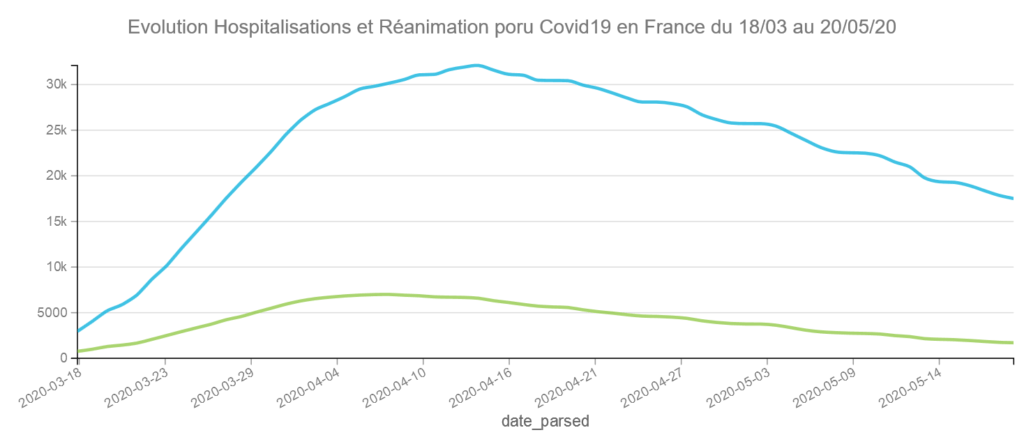
Sur l’axe des X choisissez « date_parsed », sur l’axe des Y choisissez hosp et rea. pour « date_parsed » choisissez Day comme échelle de dates, et pour hosp et rea chosissez SUM comme aggrégat. on choisira ici le graphique en lignes.

Vous remarquerez que les graphiques sont dynamiques et vous permettent d’afficher des détails en cliquant sur des points de la courbe.

Vous pouvez publier le graphique dans un tableau de bord en cliquant sur publish ou le télécharger en cliquant sur download (mais on perd l’animation comme ci-dessous)

Pour info le jour avec le plus grand nombre d’hospitalisations a été le 14 avril avec 32130 et le jour avec le plus grand nombre de réanimations le 8 avril avec 7019 cas. Depuis les courbes baissent assez lentement.

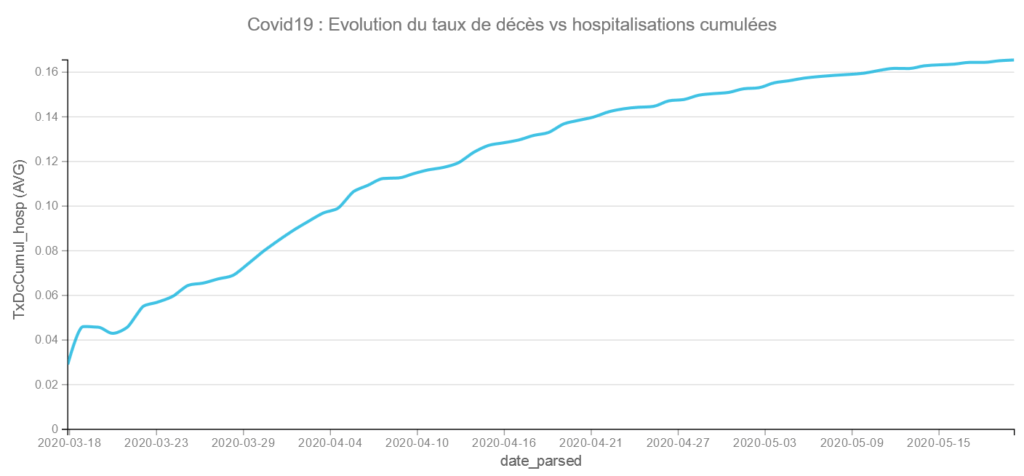
Visualisons l’évolution du Taux de décès cumulés vs hospitalisations cumulées :

on met en X les jours (date_parsed) et en Y le taux de décès vs hospitalisations cumulés sur la période (TxDcCumul_Hosp) avec un graphique en ligne

Ce taux de décès pourrait être interprété comme l’efficacité des services hospitaliers vis à vis du Covid19. Même si la courbe s’infléchit elle continue encore de grimper. Le 20/05/20, nous sommes à 16,55 % de décès vs hospitalisations en moyenne pour la France.

Comparons les départements :

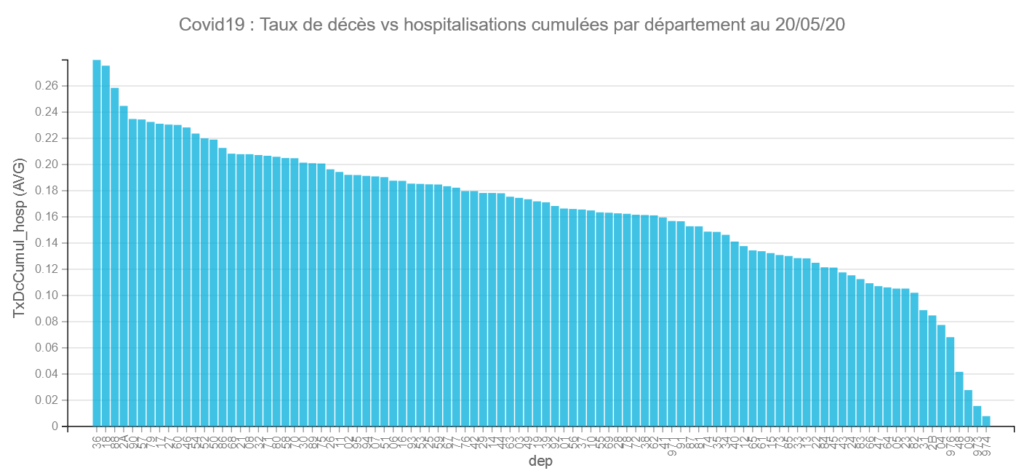
Pour cela on va mettre en X les départements (dep) en Y le Taux de décès (txDcCumul_hosp) et on filtrera sur le dernier jour (comme on a déjà un cumul). Le graphique donne les éléments suivants :

Comme on peut le voir le taux de décès vs hospitalisations varie fortement d’un département à l’autre : cela va de 27,99 % à 0,8 %.

Les départements avec les plus forts taux de décès vs hospitalisations sont l’Indre (36) 27,99 % et le Cher (18) 27,55 % , ce qui peut paraitre étrange car ces 2 départements n’ont pas été, d’après ce que l’on sait, spécialement débordés par l’épidémie.

A l’inverse les départements avec les plus faibles taux de décès vs hospitalisations sont La Réunion (974) avec 0,8 % (1 seul décès) et La Guyane (973) 1,56 % (1 décès aussi) . On peut remarquer que contrairement à ce que l’on entend par ailleurs, Mayotte (976) s’en sort pas trop mal avec 6,82%. Serait-ce la chaleur ???? 🙂

Problème de validité des Taux :

Pour éviter le biais de la loi des petits nombres (Voir Daniel Kahneman dans Système I Système II ou un résumé de biais ici), on pourrait faire des tests de proportions pour écarter les départements avec des taux non significatifs.

Vous trouverez ici une explication avec R que j’ai utilisée pour différents départements :

#test prop

######### Département les plus touchés
TotHosp <- 99114
TodDc <- 17837


#dep 36 Indre
dc <- 75
HospC <- 268
res <- prop.test(x = c(TodDc-dc, dc), n = c(TotHosp-HospC, HospC))
# Printing#the results
res #ok


#dep 18 Cher
dc <- 73
HospC <- 265
res <- prop.test(x = c(TodDc-dc, dc), n = c(TotHosp-HospC, HospC))
# Printing#the results
res #ok

#dep 974 La Réunion
dc <- 1
HospC <- 125
res <- prop.test(x = c(TodDc-dc, dc), n = c(TotHosp-HospC, HospC))
# Printing#the results
res #ok


#dep 973 - Guyane
dc <- 1
HospC <- 128
res <- prop.test(x = c(TodDc-dc, dc), n = c(TotHosp-HospC, HospC))
# Printing#the results
res #ok

#dep 976 - Mayotte
dc <- 18
HospC <- 264
res <- prop.test(x = c(TodDc-dc, dc), n = c(TotHosp-HospC, HospC))
# Printing#the results
res #ok

Problème de représentativité des échantillons des différents départements

Comme vous pouvez vous en douter, les différences sont certainement dues à des données différentes et des situations différentes dans les départements.

Afin de lever certains biais nous allons utiliser une méthode via du Machine Learning.

Pour l’instant nous avons des données sur l’age et le sexe. Nous avons aussi des informations sur la population.

Pour éventuellement avoir des indicateurs sur les taux d’occupations des lits il serait aussi intéressant de récupérer ceux-ci.

Ces informations sont disponibles dans le fichier « drees_lits_reanimation_2018.xlsx » récupéré depuis le site officiel https://drees.solidarites-sante.gouv.fr/etudes-et-statistiques/publications/article/nombre-de-lits-de-reanimation-de-soins-intensifs-et-de-soins-continus-en-france. et transformé pour n’avoir que les données de 2018.

Importez ce fichier (en faisant attention au types de variables lors de l’importation).

Vous obtiendrez un jeu de données « drees_lits_reanimations_2018« 

Nous allons « joindre » ce jeu avec notre jeu de données « covid19 » (choisir la recette « join ») au niveau du département.

Nous obtenons un nouveau jeu « covid19DepLits » que nous allons exporter dans Excel pour faire de nouveaux Traitements.

De notre côté, nous avons notamment effectué les traitements suivants :

• Ajouté les données démographiques pour Mayotte
• Calculé un taux de réanimation cumulé (à partir du taux de réa vs le taux de réanimation par jour recadré par le nombre d’hospitalisations cumulées),
• Calculé le Taux d’hospitalisations cumulées par département pour 100000 habitants pour chaque jour,
• Calculé le Taux de réanimations cumulées par département pour 100000 habitants pour chaque jour,
• Calculé un taux d’hospitalisations cumulées par lits totaux disponibles pour chaque jour,
• Calculé un taux de réanimations cumulées par lits de réanimation pour chaque jour.
• Calculé un âge moyen
• Calculé un taux de décès versus hospitalisations cumulées pour les hommes
• Calculé un taux de décès versus hospitalisations cumulées pour les femmes

Nous obtenons un fichier « covid19DepLitsProp.xlsx« .

A partir de ce fichier nous avons construit un fichier plus petit pour des raisons de manipulations et qui ne comporte que des données utiles pour la suite et notamment le Machine Learning « covid19ML.xlsx« 

Analyses Graphiques

Nous réaliserons cette étape en important le fichier covid19DepLitsProp.xlsx dans Dataiku et aussi à partir du jeu de données précédent « covid19DepLits« 

Sexe

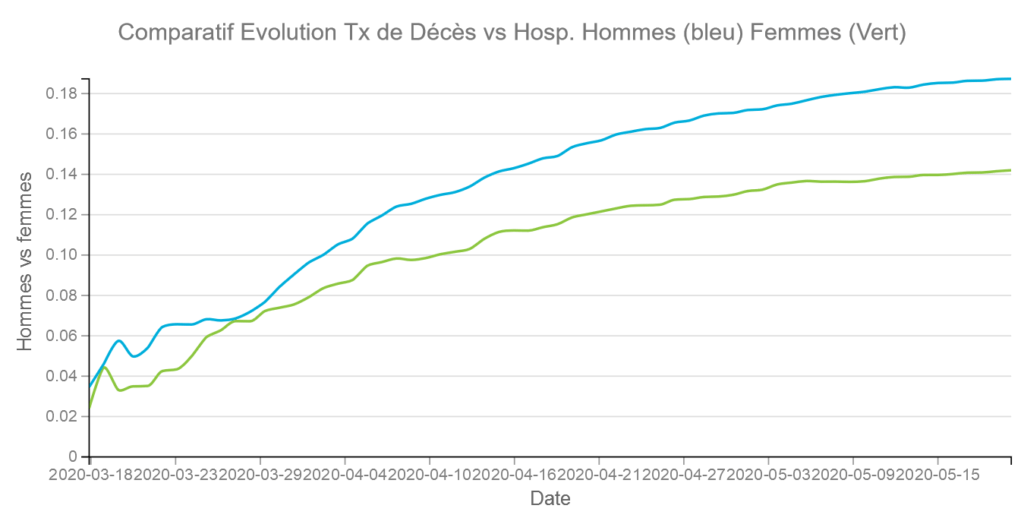
Les sexe est clairement un facteur important en terme de décès vs hospitalisations. Au 19/05 le taux de décès est de 18,73 % pour les hommes et de 14,20 % pour les femmes. Par ailleurs il a tendance à s’écarter au cours du temps.

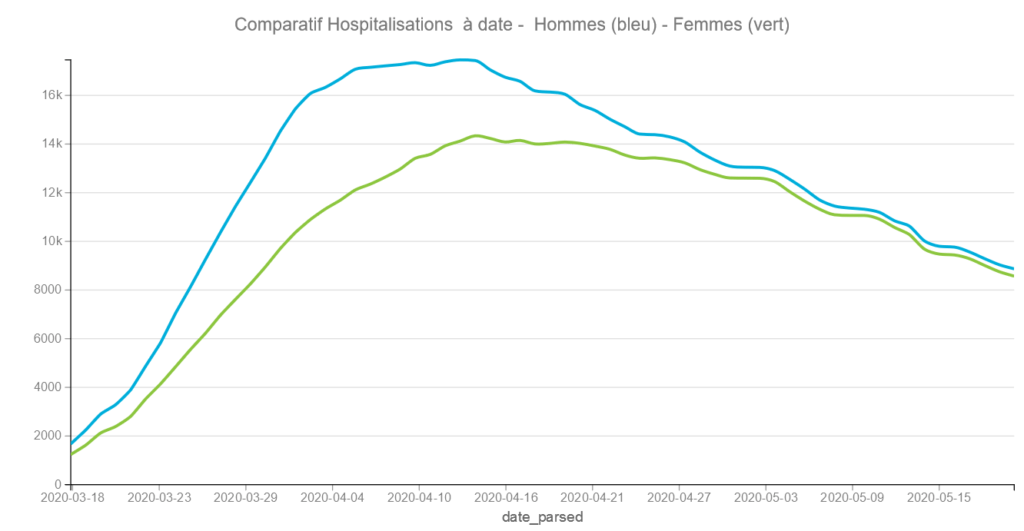
On constate qu’au cours du temps la proportion d’hommes et de femmes hospitalisés tend à s’égaliser. La courbe s’aplatit pour les hommes à partir du 6 avril et continue à monter pour les femmes jusqu’au 14 avril en ayant un décroissance moindre. Cela montre certainement que les femmes ont été plus exposées durant le confinement avec des professions en première ligne.

Comme les femmes décèdent moins il faudra faire attention à ne pas se réjouir d’un taux de décès moyen qui baisse fortement c’est peut être le fait d’avoir plus de femmes en hospitalisation.

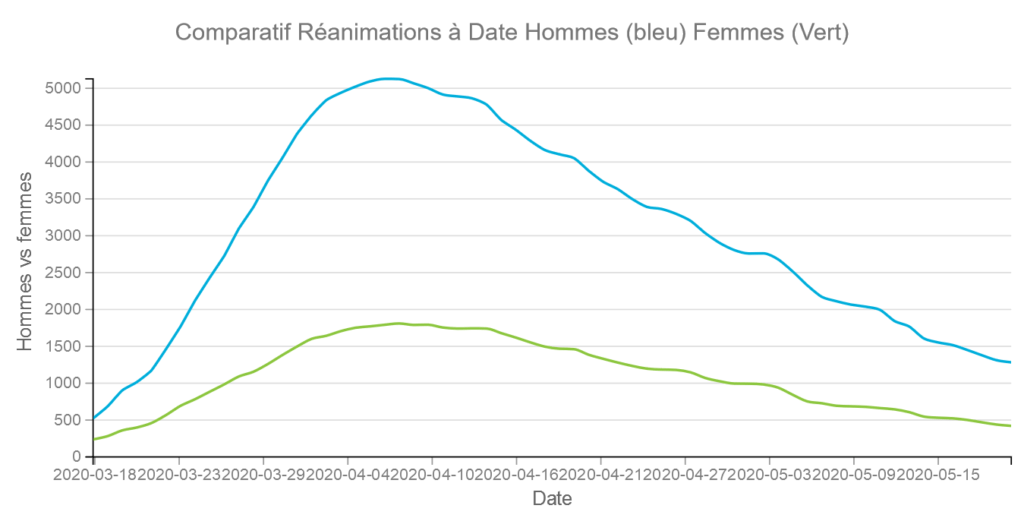
Si l’on compare par rapport au graphique précédent sur les hospitalisations on peut deviner que les hommes sont proportionnellement plus nombreux en réanimation. Ce que confirme les graphiques suivants par départements.

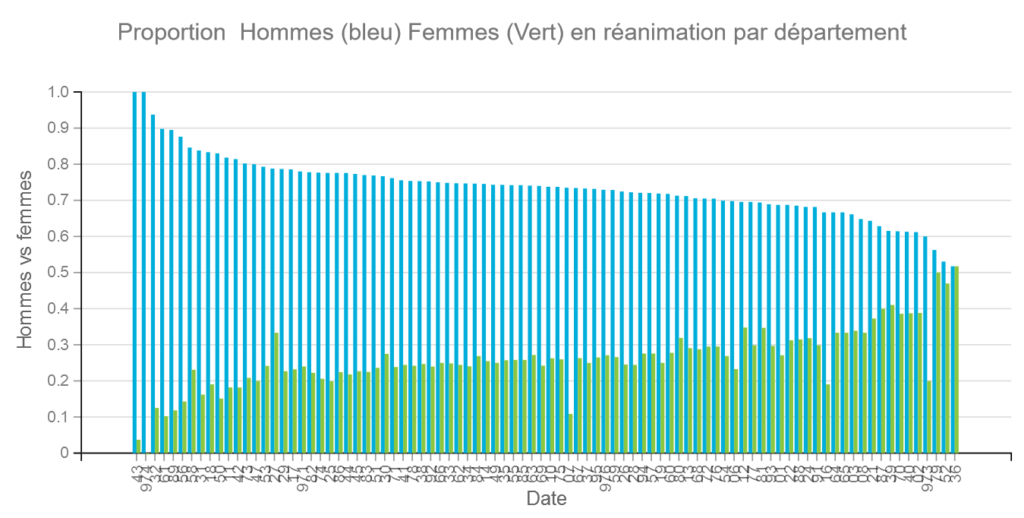
Attention la proportion d’hommes peut varier de 100% à environ 50% selon les départements. Rem : Les données de Santé Publique France étant parfois erronées le total peut dépasser ou être inférieur à 100 % .

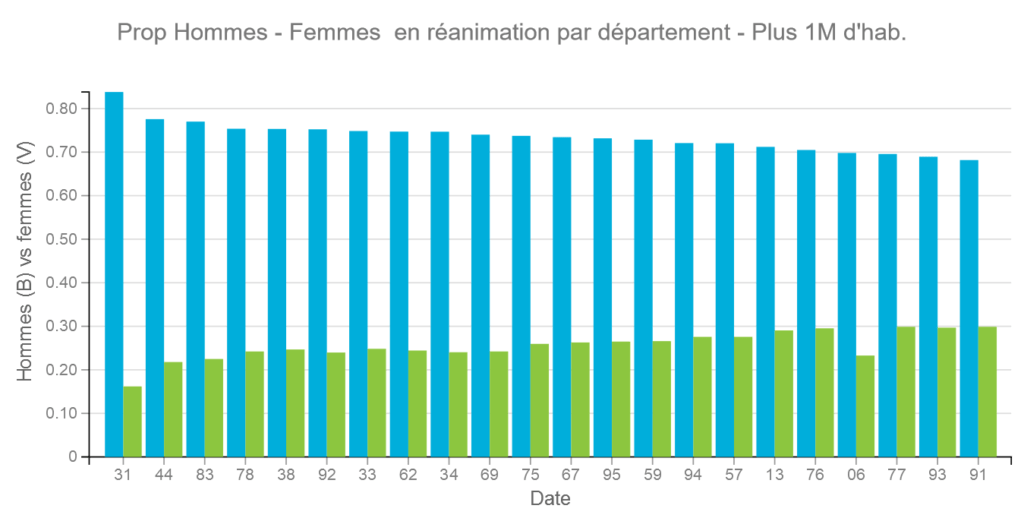
Pour les départements les plus peuplés les données sont plus homogènes.

Classes d’Age

Les classes d’âge sont les suivantes :

Code	Classe d’âge	Couleur
A	moins de 15 ans	Bleu
B	15-44 ans	Vert
C	45-64 ans	Jaune
D	65-74 ans	Orange
E	75 et plus	Rouge

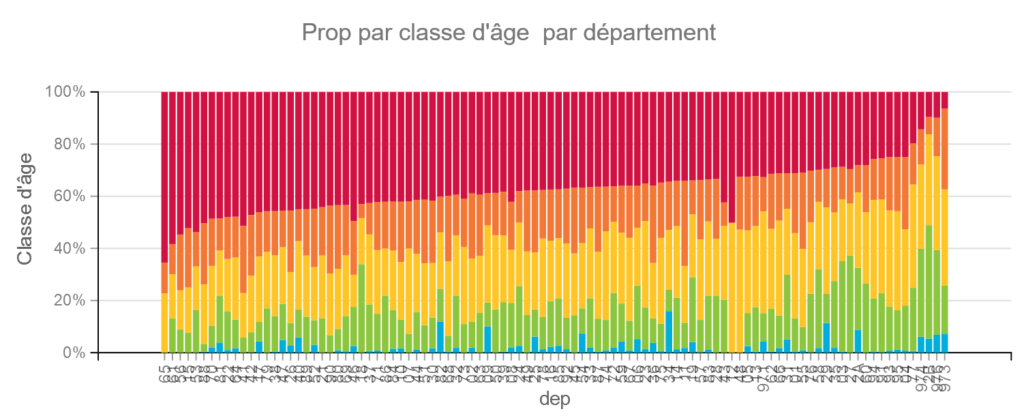
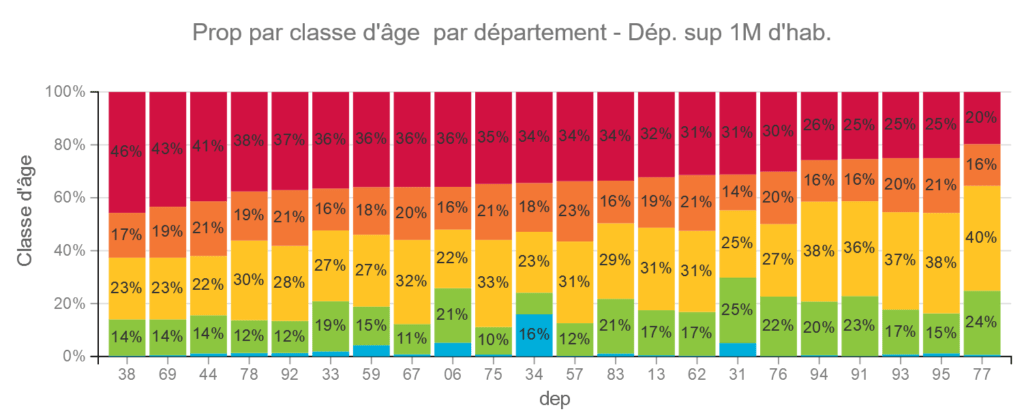
Les classes d’âge varient aussi beaucoup par département. Même si nous n’avons pas de données ici sur le taux de décès par classe d’âge, on sait par d’autres études que c’est un facteur important.

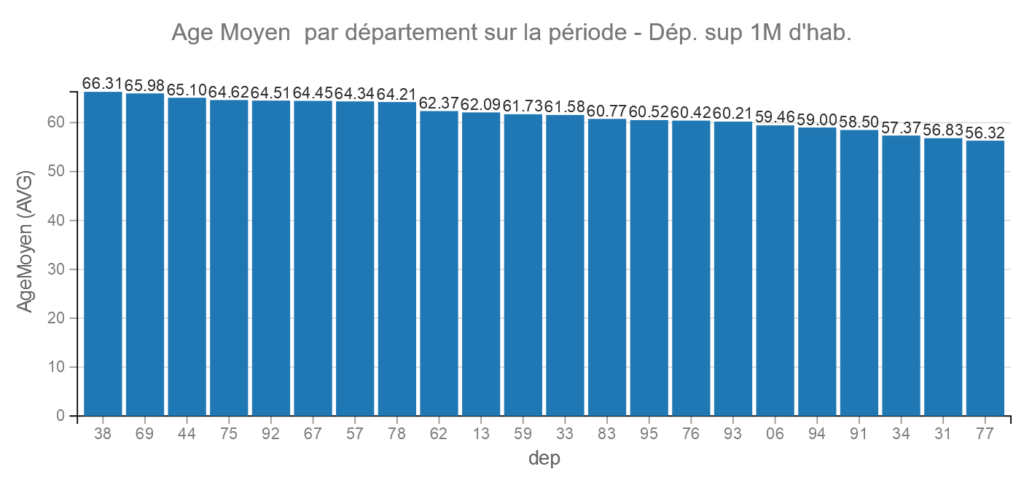
Pour les départements les plus importants, les différences s »estompent mais les populations varient tout de même beaucoup.

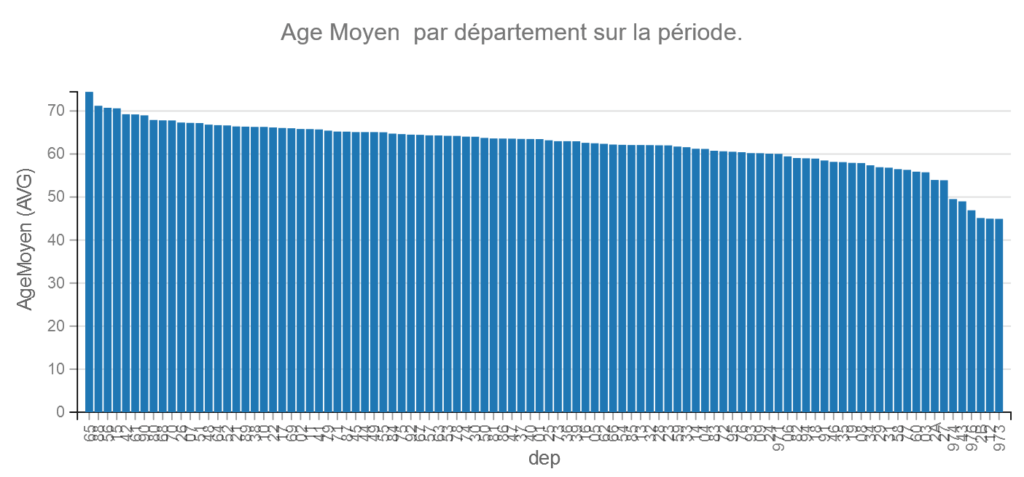
Age Moyen

Pour faciliter la visualisation nous avons créé un âge moyen à partir des médianes des classes.

Remarque la médiane de la classe plus de 75 est calculée entre 75 ans et 75 + l’espérance de vie à 75 ans. on arrive à 82 ans.

Analyses via Machine Learning dans Dataiku

Dataiku permet de réaliser des analyses rapidement et de faire tourner plusieurs algorithmes de Machine Learning facilement.

Ceci permet d’éviter de créer un programme en R ou en Python

Préparation des données avant analyse :

Commencez par uploader le fichier « covid19ML.xlsx » dans Dataiku. Attention à veiller aux types de données.

Nous obtenons un jeu de données « covid19ML »

Lors des calculs, nous aurons besoin de pondérer les données en fonctions de la variables « hospCumul » qui dénombre les « individus » de notre jeu par jours.

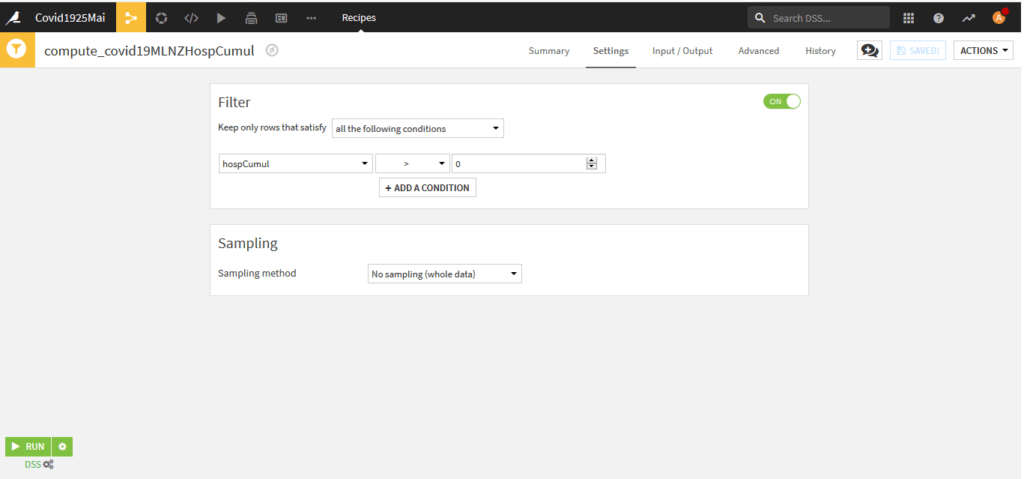
Afin d’éviter des divisions par zéro il est nécessaire de supprimer les enregistrements avec hospCumul=0. Pour cela nous allons utiliser la recette « Sample/Filter »

Le nom de notre jeu de données en sortie est « covid19MLNZHospCumul« .

Première Analyse – Par département

Dans le menu en haut à gauche choisissez le logo qui ressemble à une roue et ensuite « Visual Analyses » puis « +New Analysis » :

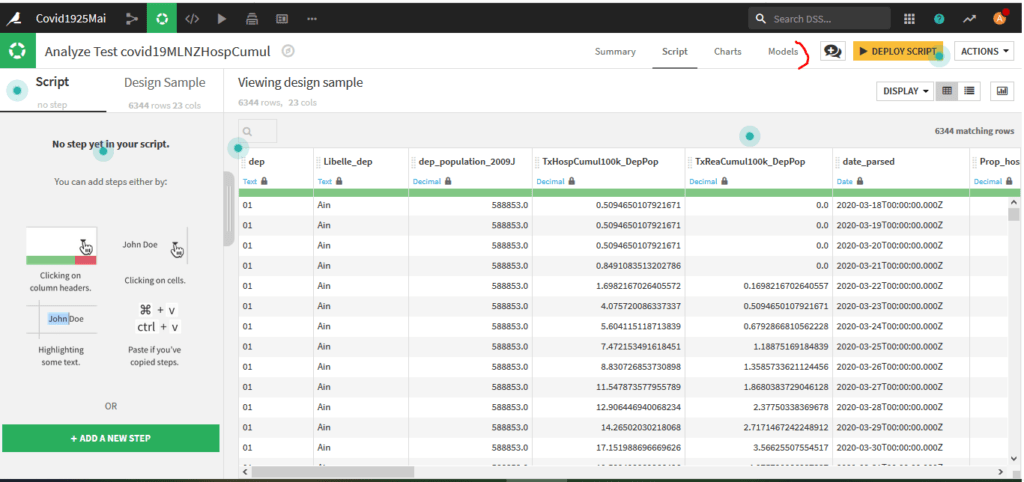
Choisissez ensuite le jeu de données à analyser, pour nous « covid19MLNZHospCumul » et donnez un nom à votre analyse.

Vous arrivez sur la page d’accueil de votre analyse avec votre jeu de données :

Cliquez en haut à droite sur « Models » pour définir votre premier modèle. La première fois que vous créer un modèle vous passer par différents écrans :

• Create First Model
• Prediction
• Choisir la variable à expliquer ici « TxDcCumul_hospCumul« 
• Expert Mode
• Create

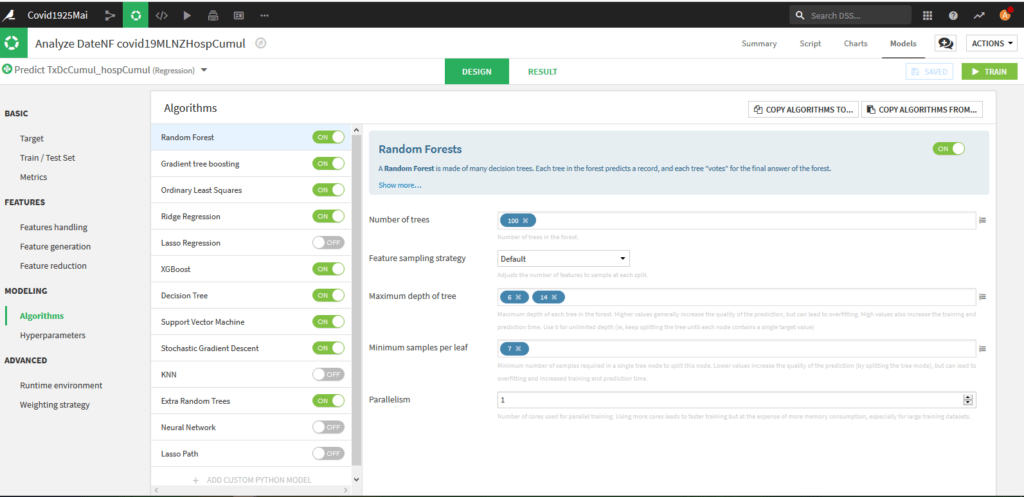
Normalement vous arrivez sur la page de Design dans l’onglet « Algorithms »

Choisissez les algorithmes, au moins Random Forest et XGBoost qui sont en général ceux qui fonctionnent le mieux et Ordinary Least Squares et Ridge Regression qui sont des modèles linéaires plus facilement interprétables.

Attention les modèles Lasso Regression, KNN, Neural Network et Lasso Path ne fonctionnent pas avec l’option de pondération dont nous avons besoin.

Allons voir les autres onglets :

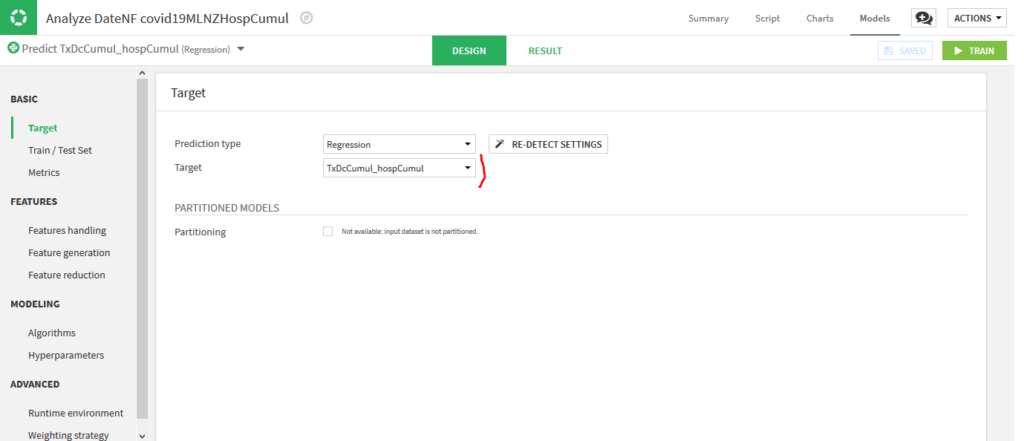
BASIC -> Target :

On voit ici la variable cible que l’on avait choisie « TxDcCumul_hospCumul« . Ne pas changer les options.

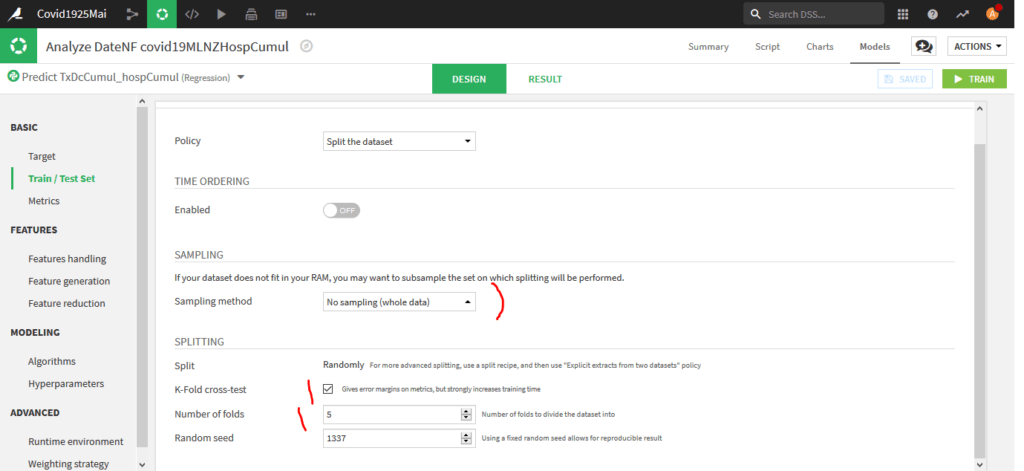
BASIC -> Train / Test Set :

Choisissez No Sampling pour Sampling Method et K-Fold cross-test et laisser 5 comme nombre de folds (découpages).

Pour BASIC -> Metrics on restera sur le R2 Score (par défaut)

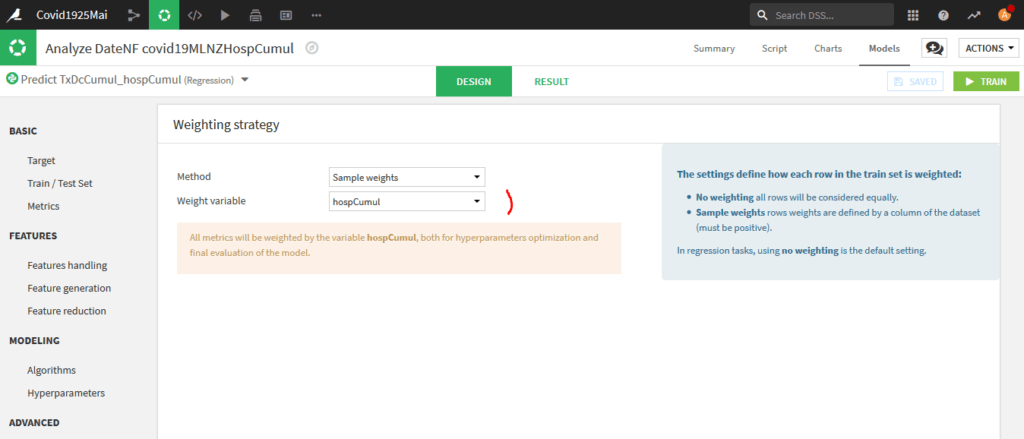
ADVANCED -Weighting Strategy :

Pondérez sur la variable « hospCumul ».

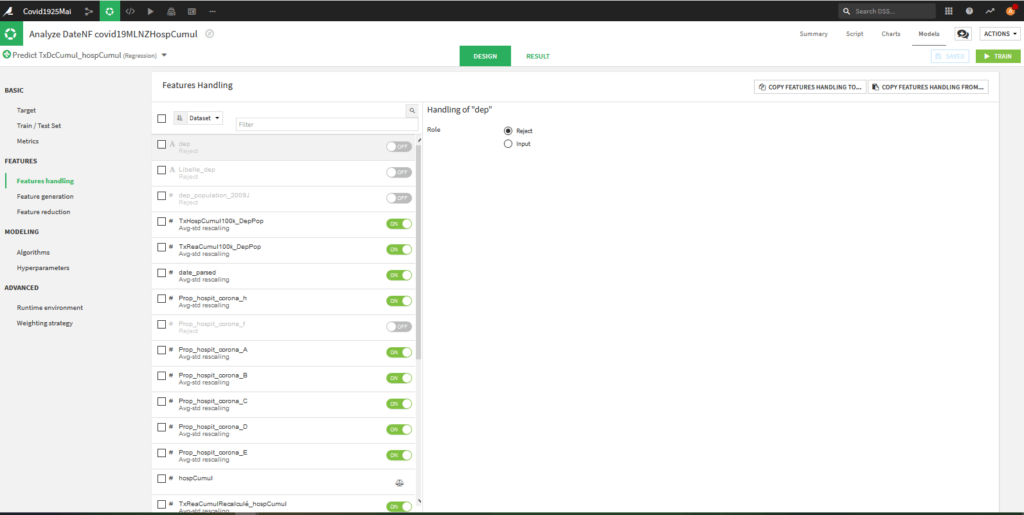
Features -> Features Handling :

On va déterminer les caractéristiques de notre modèle ou les variables explicatives.

Pour notre part, nous avons choisi d’inclure la Date car les données évoluent fortement dans le temps. Sinon nous avons pris les variable Taux et Proportions sauf pour les femmes « _f » car l’information fait plus ou moins doublon avec les hommes et que cela générait des variables non significatives dans les modèles linéaires.

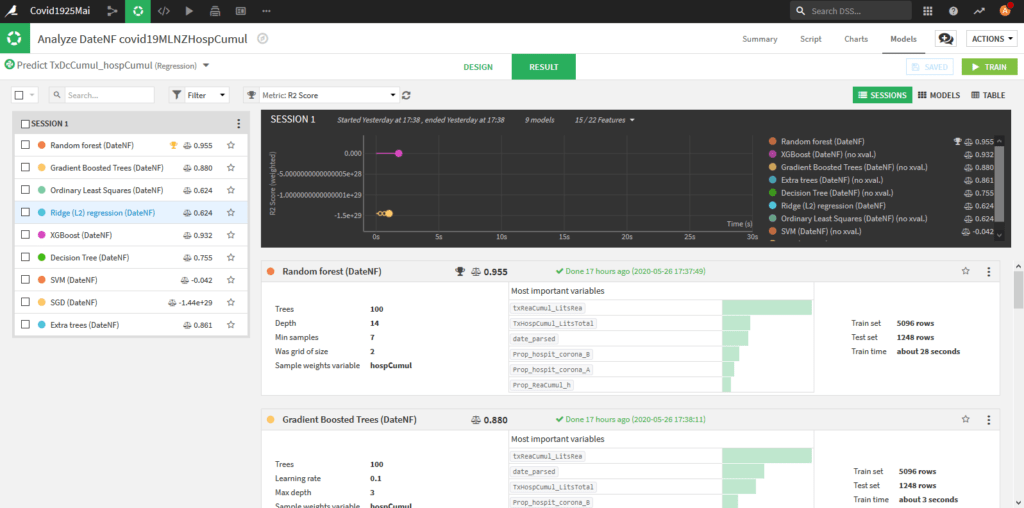
Une fois que vous avez fini vos paramétrages appuyez sur Train et donnez un nom à votre analyse. Le système bascule sur la page « Result »

A gauche, vous avez les différents algorithmes avec leurs scores, comme vous pouvez le constater, dans notre cas c’est Random Forest qui obtient le meilleur score.

En cliquant sur le nom de l’algorithme, on peut aller voir les détails des résultats pour celui-ci. on présentera quelques données dans le paragraphe suivant.

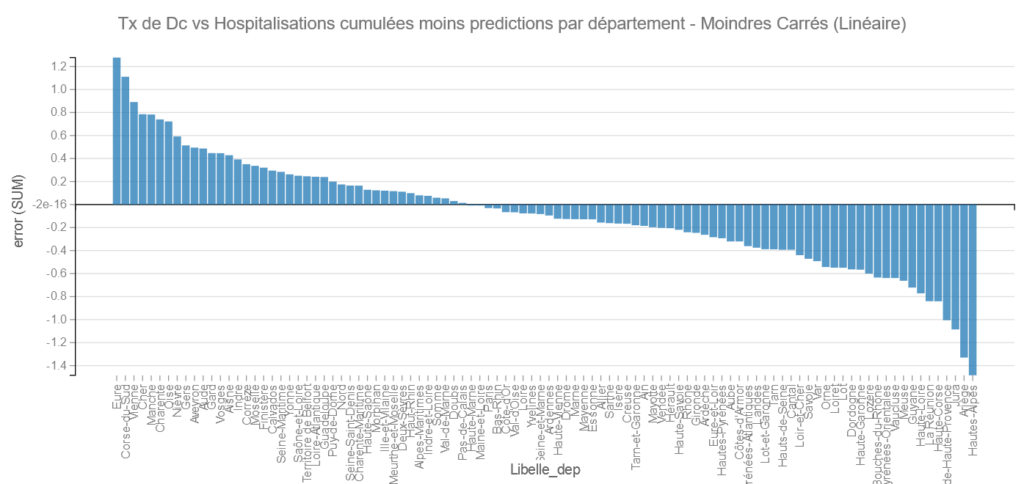
Résultats par Modèles et Départements :

NB : plus l’erreur est petite (et négative) plus le Tx De décès vs Hospitalisations réel est meilleur que le modèle théorique.

Moindres Carrés (Ordinary Least Square) :

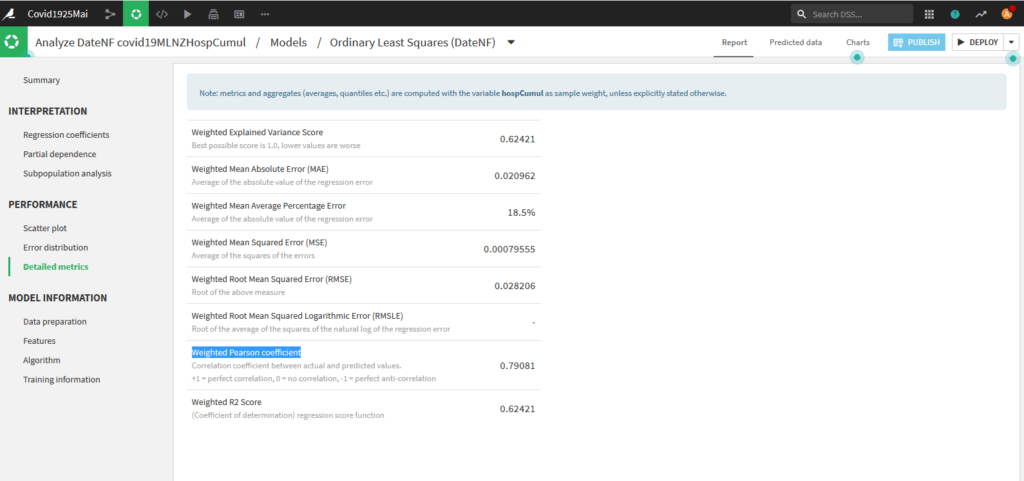
Cette méthode est linéaire, allons voir ses performances sur la page Performance – Detailed Metrics :

A près de 0,8 le coefficient de Pearson montre que le modèle est déjà très correct.

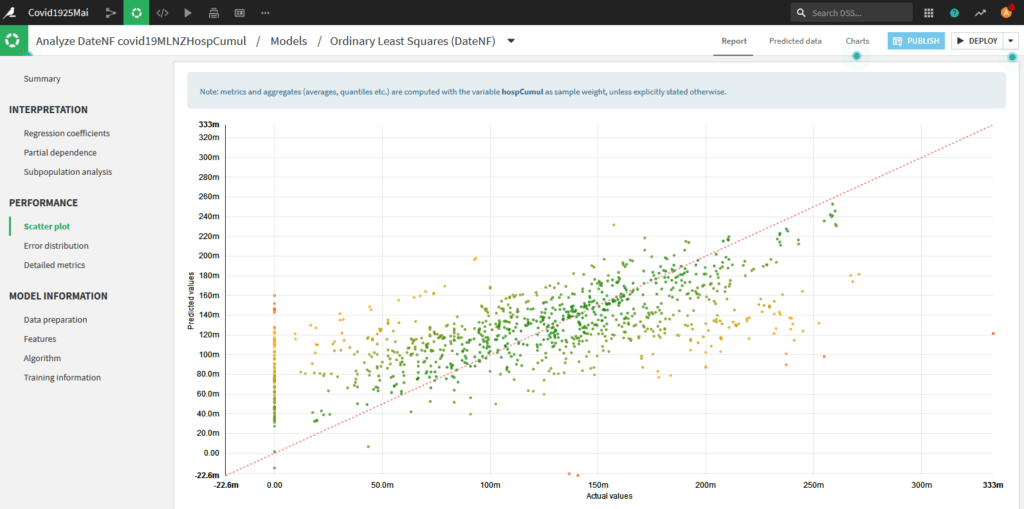
Toutefois, le graphique en nuage de points est assez moyen :

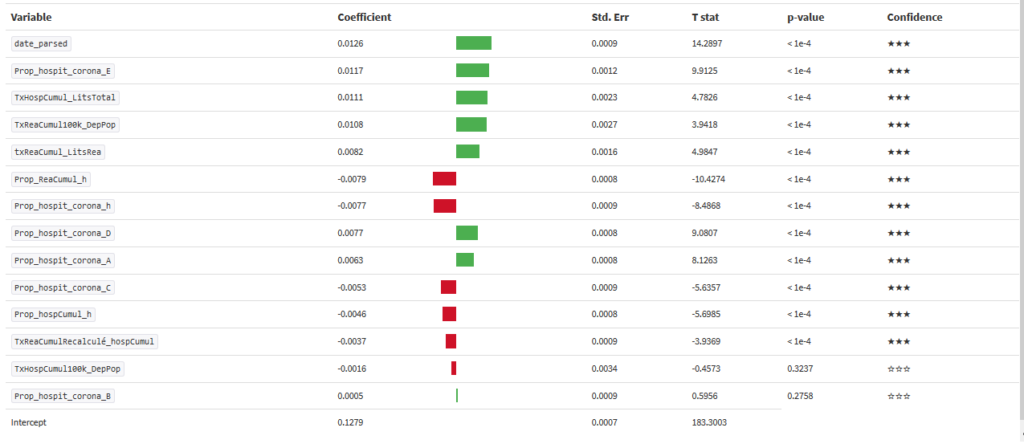
Comme le modèle est linaire on peut afficher les coefficients de régression :

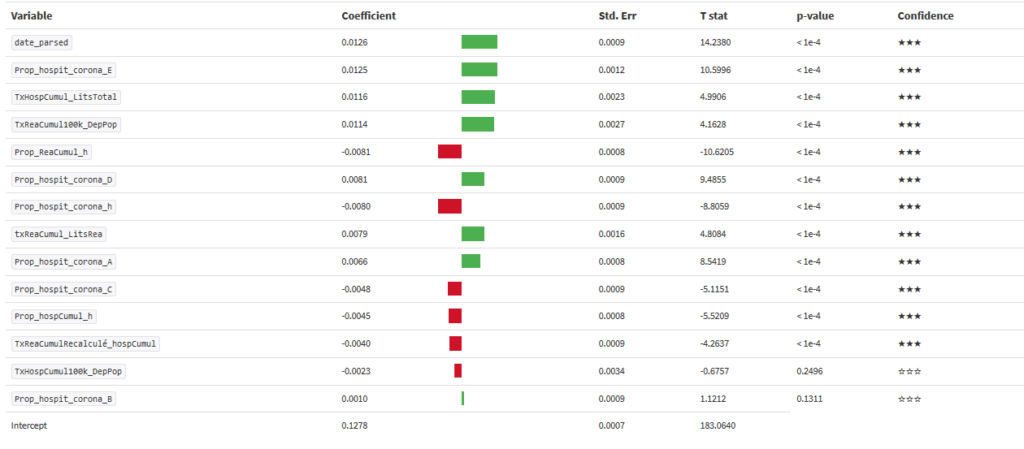
Mis à part la date (ce qui est logique) les facteurs contribuant au décès sont le fait d’avoir plus de 75 ans, le taux d’hospitalisation par rapport au nombre de lits au départ, le taux de personnes en réa cumulé pour 100000 habitants.

En cliquant sur « Predicted Data » vous avez accès aux données de Prédiction et sur « Charts » vous pouvez faire des graphiques sur ces prédictions.

La variable qui nous intéresse est la variable « error« 

Pour cet Algorithme ce sont les Hautes-Alpes et l’Ariège qui s’en sortent le mieux et L’Eure et la Corse du Sud le moins bien. (Sous réserve de validité – voir plus haut)

Remarque : comme les grands départements participent le plus au modèle il y a des chances qu’on les retrouve plutôt vers le centre.

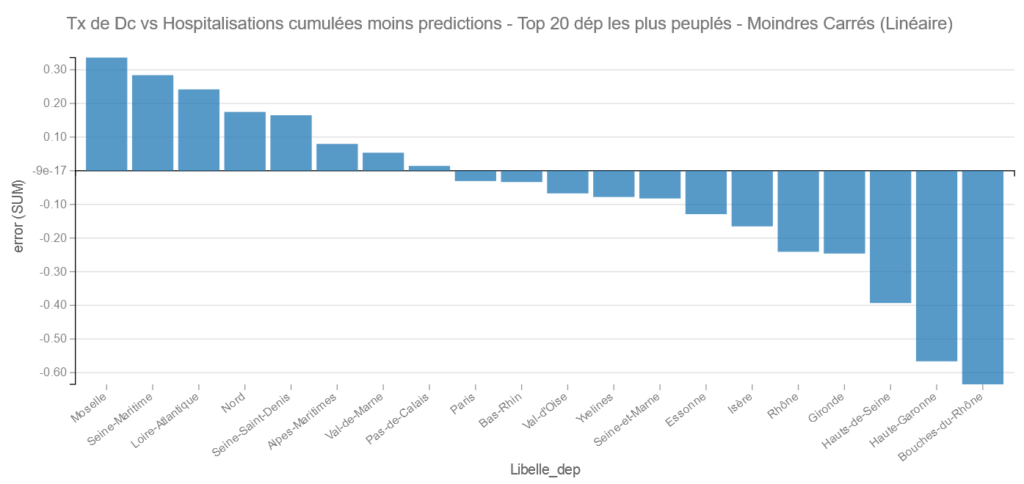
Pour les départements les plus peuplés, on retrouve Les Bouches du Rhône et la Haute-Garonne comme bons élèves et La Meuse et la Seine Maritime comme les moins bons.

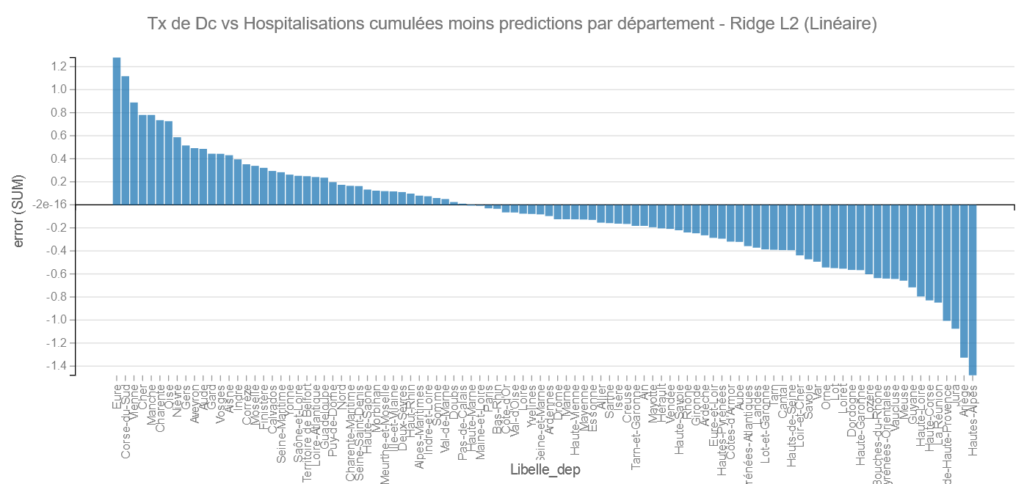
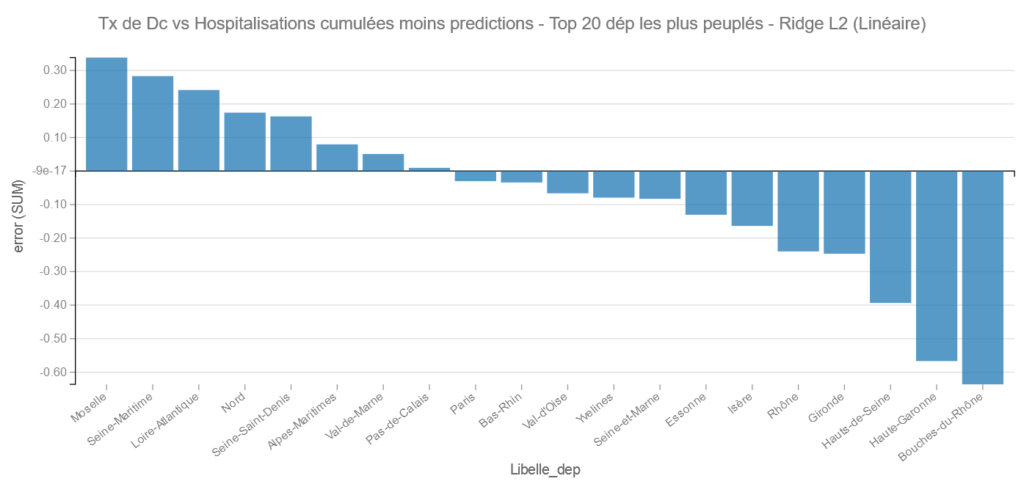
Ridge L2 :

Comme Ridge est un modèle linéaire on peut aussi récupérer les coefficients de régression :

Comme pour les moindres carrés on retrouve comme facteurs importants : le fait d’avoir plus de 75 ans, le taux d’hospitalisation par rapport au nombre de lits au départ, le taux de personnes en réa cumulé pour 100000 habitants.

Regardons la position des départements :

Comme précédemment on retrouve les Hautes Alpes et l’Ariège dans les bons élèves et L’Eure et La Corse du Sud dans les moins bons.

Pareil Les Bouches du Rhône et la Haute Garonne du bon côté et la Moselle et la Seine Maritime du mauvais.

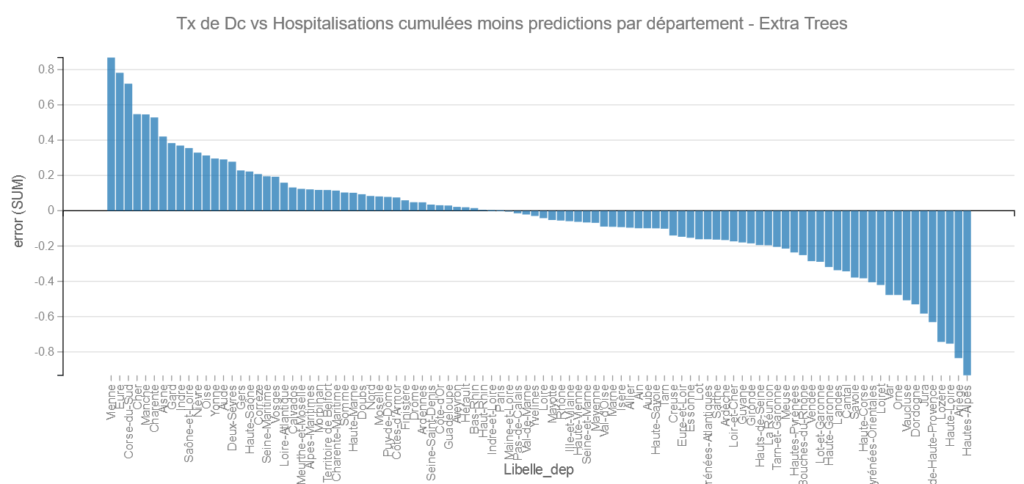
Extra Trees :

Ce modèle permet de récupérer l’importance des variables c’est à dire celles qui « expliquent » le plus le modèle.

Ici les variables liées à la saturation des hôpitaux expliquent mieux le modèle que les variables d’âge et bien plus que les variables liées au sexe.

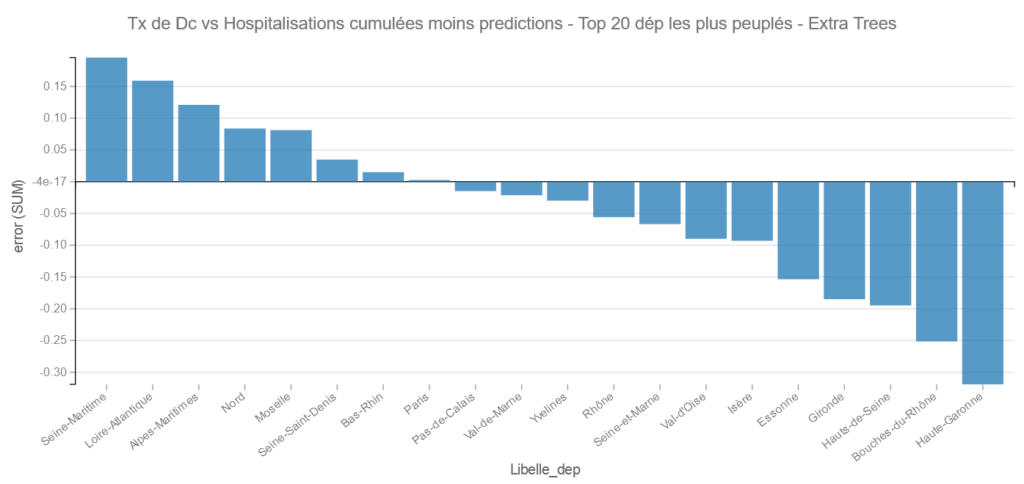
On retrouve les Hautes-Alpes et l’Ariège dans les bons élèves et cette fois la Vienne et encore l’Eure dans les mauvais.

Pour les grands départements : Cette fois c’est la Haute-Garonne qui fait mieux que les Bouches du Rhône et pour les moins bons la Seine Maritime et La Loire-Atlantique.

Random Forest :

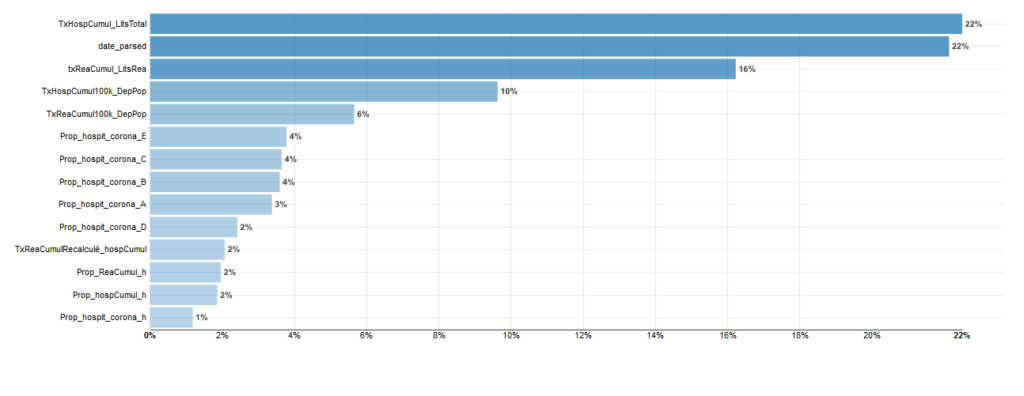
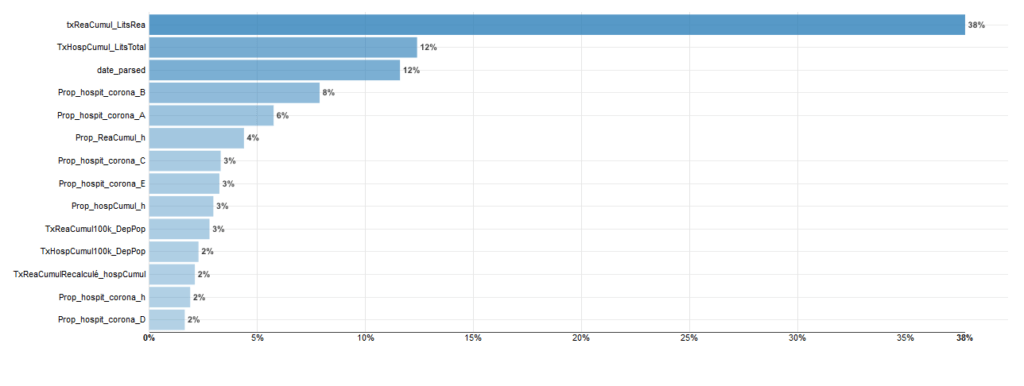
Ce modèle est celui qui a donnée le meilleur R2 Score soit 0.955. On peut aussi récupérer l’importance des variables.

Comme vous pouvez le constater le Taux de saturation de lits de réanimation explique à lui tout seul 38% du modèle.

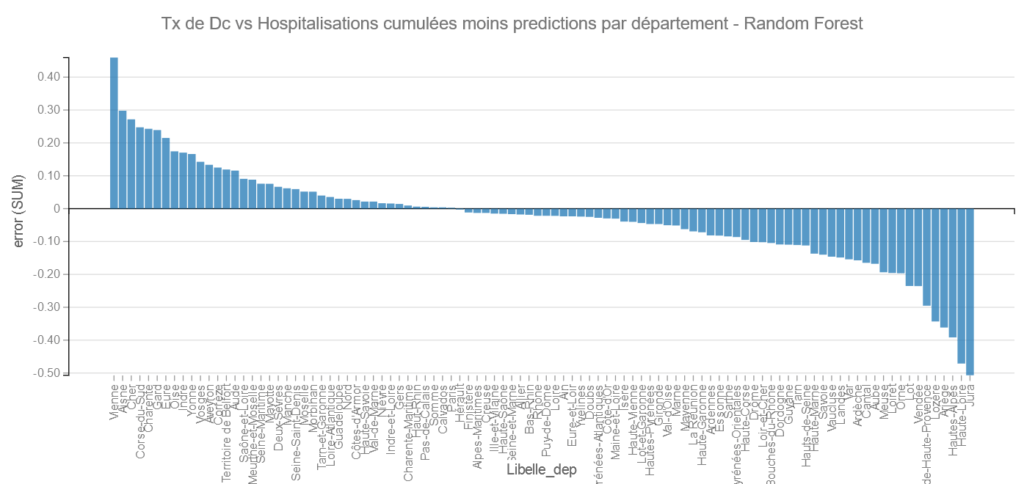
Pour Random Forest les bons élèves sont le Jura et la Haute-Loire et les mauvais La Vienne et l’Aisne.

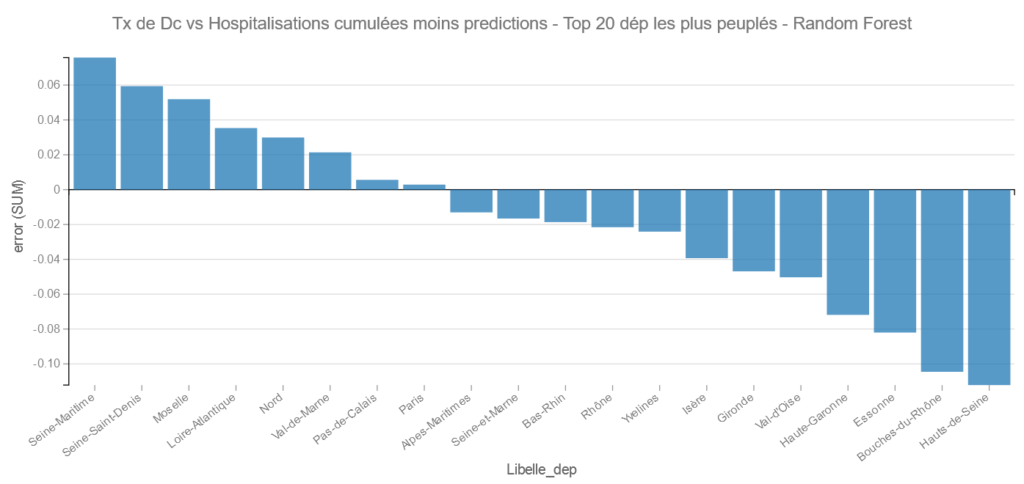
Dans les départements les plus peuplés on retrouve ici les Hauts-de-Seine et les Bouches du Rhône en bons élèves et la Seine Maritime et la Seine-Saint Denis dans les moins bons.

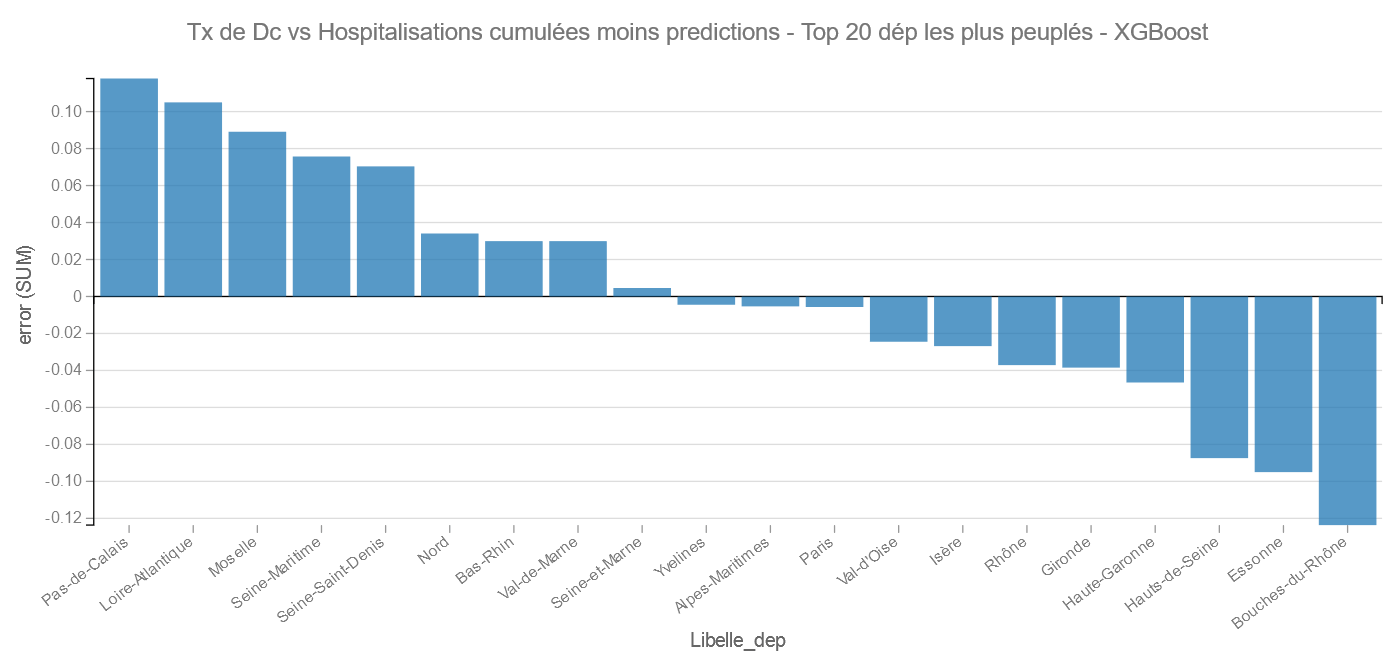
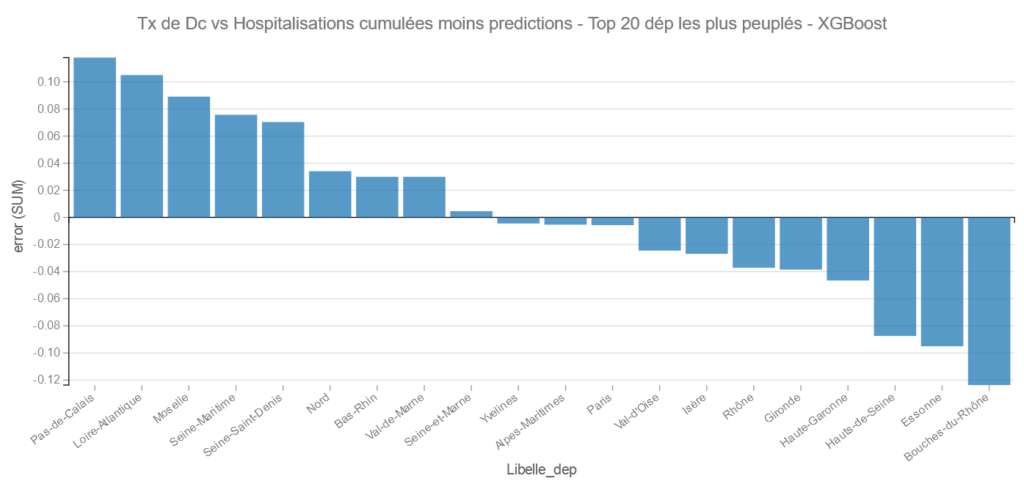
XGBoost :

On peut aussi afficher l’importance des variables pour XGBoost :

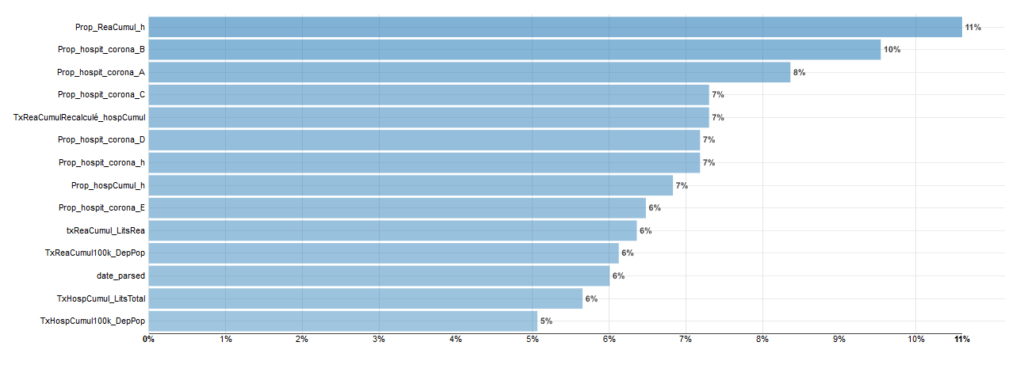
XGBoost propose une répartition plus équilibrée de l’importance des variables.

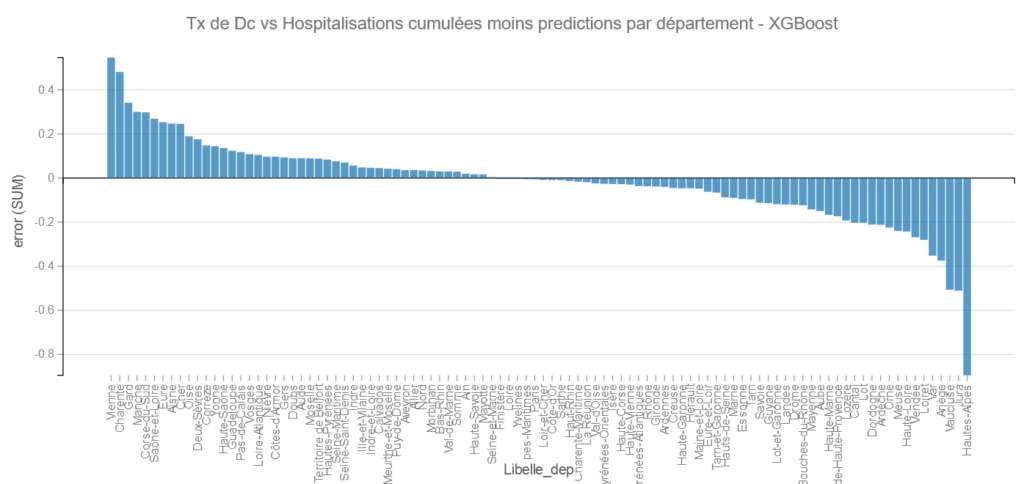
Pour XGBoost on retrouve les Hautes-Alpes et le Jura comme bons élèves et La Vienne et la Charente dans les moins bons.

Pour les grands départements on retrouve encore Les Bouches du Rhône suivi de l’Essonne comme bon élève et le Pas de Calais et la Loire-Atlantique comme moins bon.

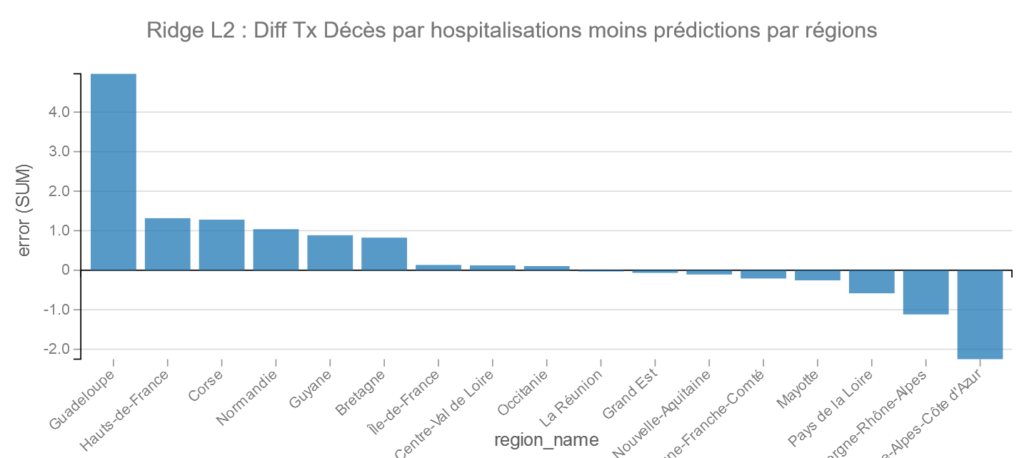
Résultats par Modèles et régions

Pour construire le jeu de données par Région nous avons fait un « join » grâce au fichier « departements-region.csv » puis ensuite un « Group By » sur les régions et les jours.

Les résultats sont les suivants :

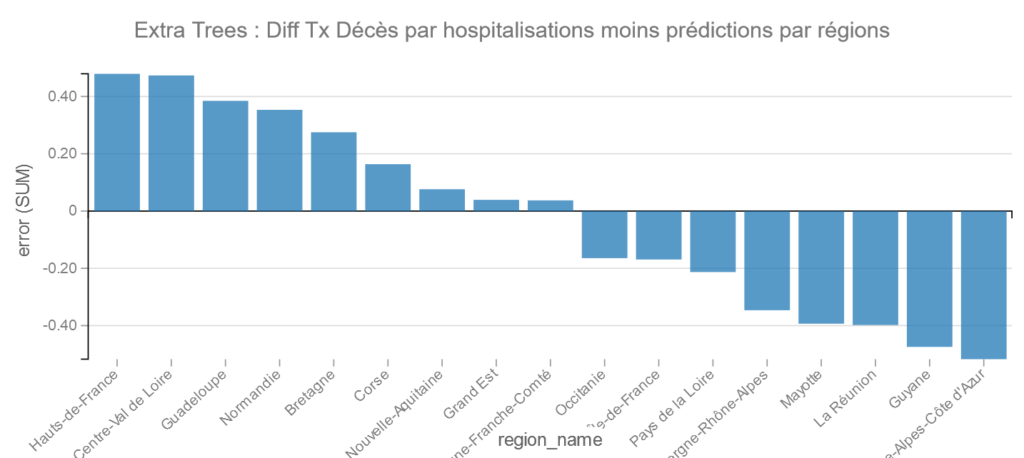
Extra Trees

Dans les bons élèves PACA et la Guyane et pour les moins bons les Hauts de France et le Centre Val de Loire.

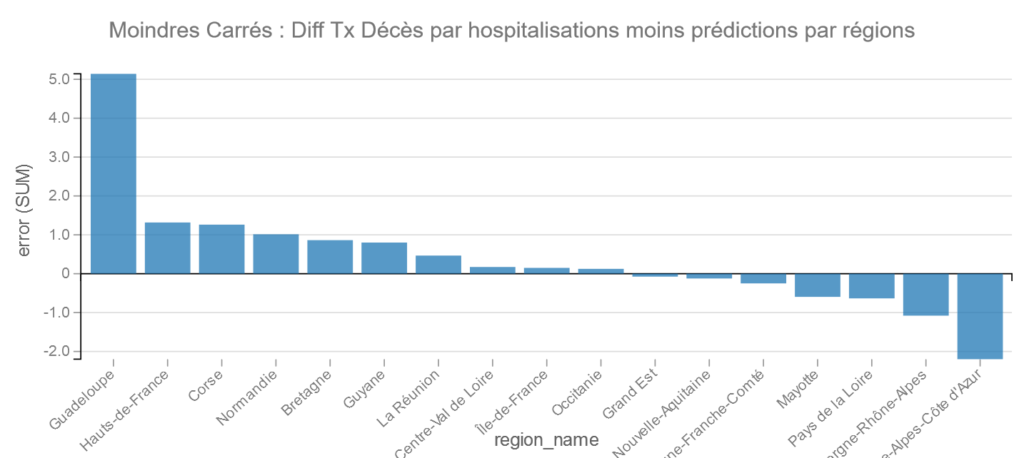
Ordinary Least Squares

Pour les Moindres Carrés on retrouve PACA suivi de Auvergne-Rhône-Alpes dans les bons élèves et la Guadeloupe et les Hauts-de-France dans les moins bons.

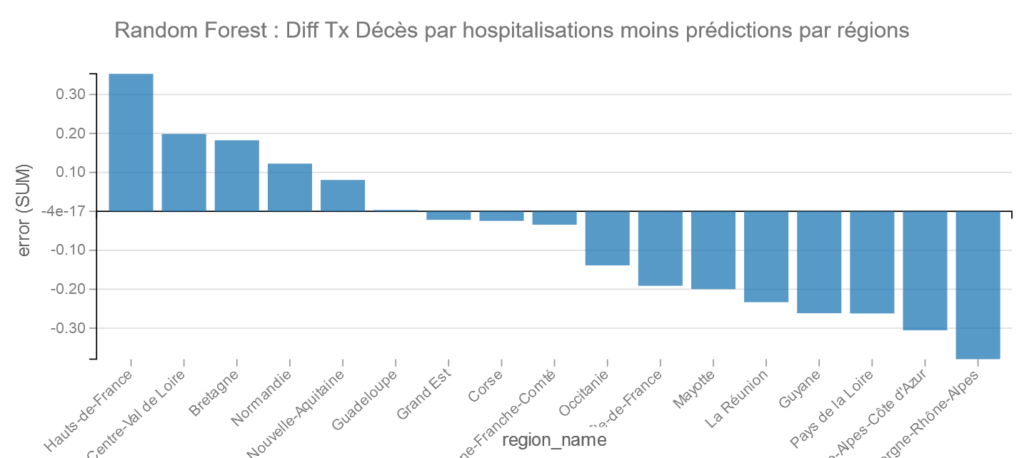
Random Forest

Pour Random Forest Auvergne-Rhône-Alpes fait mieux que PACA et les moins bons sont les Hauts-de-France et Centre-Val de Loire.

Ridge L2 :

Pour Ridge on retrouve la mêms chose que pour les Moindres Carrés : PACA suivi de Auvergne-Rhône-Alpes dans les bons élèves et la Guadeloupe et les Hauts-de-France dans les moins bons.

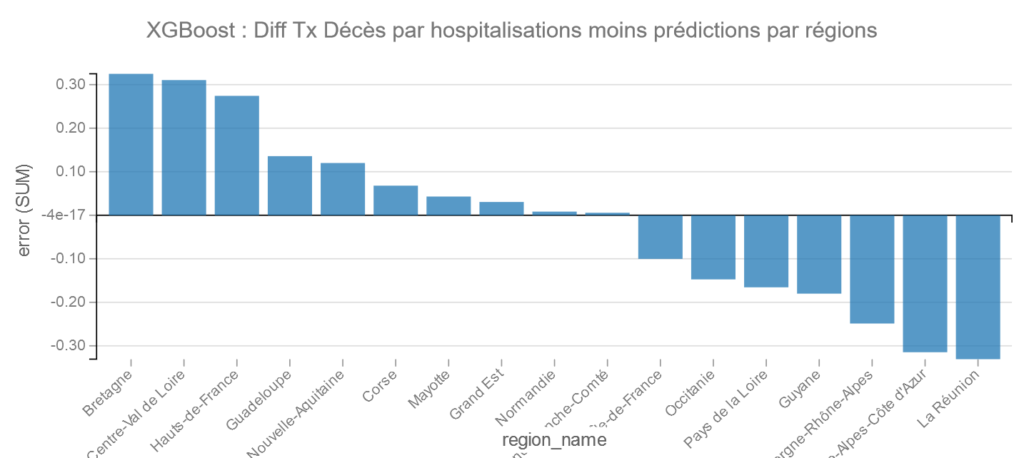
XGBoost :

Pour XGBoost La Réunion fait le meilleurs score suivi de PACA, et ce sont la Bretagne et le Centre Val de Loire qui font le moins bon score.

Conclusion Provisoire

A ce stade nous n’avons malheureusement pas de données précises sur les traitements et notamment concernant la consommation de Chloroquine et d’Hydroxychloroquine qui fait débat.

Je n’ai trouvé qu’une étude sur le sujet (mais sans les chiffres) provenant de la CNAM et dont parle Libération.

On notera toutefois ce que dit la CNAM :

« Mais c’est en Paca qu’il y a proportionnellement le plus de patients incidents. «Il y a probablement eu une croyance plus élevée dans l’efficacité présumée de la chloroquine et de l’hydroxychloroquine dans le Covid-19 en région Paca, région du P^r Didier Raoult, promoteur de la chloroquine et de l’hydroxychloroquine», commente la Cnam. »

Libération

En conclusion, pour l’instant au vu de ces éléments et compte tenu des éléments exposés ci-dessus par nos soins, il n’existe pas de preuve de surmortalité dans les Bouches du Rhône et en PACA malgré une consommation plus importante de la chloroquine et de l’hydroxychloroquine (d’après la CNAM), tout au contraire.

Nous avons par ailleurs noté que les variables liées aux hôpitaux et au stade dans l’épidémie (comme les niveaux de saturation des services de Réanimations) sont souvent plus importantes que les variables individuelles pour expliquer le taux de décès.

Nous en profitons pour noter que dans l’étude publiée le 22 mai 2020 dans le Lancet : « Hydroxychloroquine or chloroquine with or without a macrolide for treatment of COVID-19: a multinational registry analysis« , les facteurs de ce type ne semblent pas avoir été utilisés, ce qui à notre sens, peut biaiser grandement les résultats.

Il conviendra de notre côté d’affiner notre modèle, notamment à partir de données complémentaires.

La suite de cet article : https://www.anakeyn.com/2020/06/11/etude-donnees-hospitalieres-covid-19-ii/

Et vous qu’avez-vous trouvé ? Commentaires bienvenus.

A Bientôt,

Pierre