Partager la publication "Classification de pages via le Machine Learning sur un univers de concurrence avec Python – II"
Cet article fait suite aux 5 articles précédents :
- Classification de pages Web pour le SEO via le Machine Learning avec Python
- Récupérez des données de positionnement de vos pages via Google Search Console API
- Modèle Interne : test de classification de pages via le Machine Learning pour un seul site
- Classification de pages via le Machine Learning sur un univers de concurrence avec Python – I.
- Scraping des pages Web pour enrichissement avant Machine Learning
Dans cet article nous allons refaire un essai de Machine Learning sur un univers de concurrence à partir des données que nous avions enrichies dans l’article précédent.
Pour ce faire nous allons re-tester les algorithmes que nous avions utilisés précédement : K-NN (k plus proches voisins), LogisticRegression et LinearSVC ainsi que Ridge, Lasso et ElasticNet. Nous allons aussi tester l’algorithme XGBoost que nous avions utilisé dans une série d’articles précédents sur le Machine Learning avec R.
Algorithmes Ridge, Lasso et ElasticNet
Les modèles Ridge, Lasso et Elasticnet font partie des modèles linéaires « régularisés ».
Pour résumer, il s’agit de modèles dont on peut faire varier des paramètres qui permettent d’éviter la sur-optimisation sur les données d’entrainement.
Algorithme XGBoost
L’algorithme XGBoost (pour eXtrem Gradient Boosting) est un algorithme d’apprentissage machine supervisé. Actuellement très à la mode, il donne souvent de très bons résultats par rapport à d’autres algorithmes.
Plus complexe que les modèles linéaires précédents, il n’est pas très aisée d’expliquer facilement comment cela fonctionne.
Pour faire simple, disons que le « boosting » singe les règles de l’apprentissage : le boosting consiste à faire des essais/erreurs et de sélectionner ce qui marche.

La méthode derrière le boosting est basée sur des arbres de décisions comme par exemple dans le modèle Random Forest.
La différence fondamentale est que Random Forest crée plusieurs arbres en parallèle et ensuite on construit la meilleure solution à partir de tous les arbres créés. Cela se fait selon un « vote majoritaire », ce qui veut dire que tous les arbres ont le même poids dans le calcul. On ne considère pas qu’il y en a de meilleurs que d’autres..
Le boosting se fait de façon séquentielle. A chaque itération l’arbre de décision s’améliore car il tient compte des erreurs précédentes et va les corriger. Du fait de ces calculs à chaque itération, il peut être plus lent que Random Forest.
Le gradient boosting utilise une méthode dite de « descente du gradient » (ou plus forte pente) pour minimiser cette erreur à chaque itération.
Remarque : on parle aussi de notion de coût pour l’erreur et de fonction de coût pour la fonction qui calcule cette erreur.
eXtrem Gradient Boosting est un version sophistiquée du Gradient Boosting et est implémentée dans Python.
XGBoost comporte de nombreux paramètres et donne des résultats très différents selon ceux-ci. C’est pourquoi nous verrons dans un prochain article comment optimiser ces paramètres de façon automatique.
De quoi aurons nous besoin ?
Python Anaconda
Comme précédemment, téléchargez la version de Python Anaconda qui vous convient selon votre ordinateur.
Jeu de données
Téléchargez le jeu de données des Requêtes/Pages/Positions sur Github : https://github.com/Anakeyn/GSCCompetitorsMachineLearning2/raw/master/dfQPPS7.csv
Code Source
Vous pouvez soit copier/coller les morceaux de codes ci-dessous, soit récupérer le code source en entier gratuitement dans notre boutique : https://www.anakeyn.com/boutique/produit/script-python-donnees-enrichies-ml-concurrence-ii/
Chargement des bibliothèques utiles
# -*- coding: utf-8 -*- """ Created on Mon Jul 1 10:29:18 2019 @author: Pierre """ ########################################################################## # GSCCompetitorsML2 - Modifié le 26/11/2019 # Auteur : Pierre Rouarch - Licence GPL 3 # Machine Learning sur un univers de concurrence 2 #Données enrichies via Scraping précédemment. récupérées via le fichier dfQPPS7.csv allégé. # focus sur la précision du test au lieu du F1-Score global ##################################################################################### ################################################################### # On démarre ici ################################################################### #Chargement des bibliothèques générales utiles import numpy as np #pour les vecteurs et tableaux notamment import matplotlib.pyplot as plt #pour les graphiques #import scipy as sp #pour l'analyse statistique import pandas as pd #pour les Dataframes ou tableaux de données #import seaborn as sns #graphiques étendues #import math #notamment pour sqrt() import os # Machine Learning from sklearn.neighbors import KNeighborsClassifier from sklearn.linear_model import LogisticRegression from sklearn.svm import LinearSVC from xgboost import XGBClassifier from sklearn.linear_model import Ridge from sklearn.linear_model import Lasso from sklearn.linear_model import ElasticNet from sklearn.model_selection import train_test_split from sklearn.preprocessing import StandardScaler #pour les scores from sklearn.metrics import f1_score #from sklearn.metrics import matthews_corrcoef from sklearn.metrics import accuracy_score print(os.getcwd()) #verif #mon répertoire sur ma machine - nécessaire quand on fait tourner le programme #par morceaux dans Spyder. #myPath = "C:/Users/Pierre/MyPath" #os.chdir(myPath) #modification du path #print(os.getcwd()) #verif
Détermination des variables et préparation des données
#############################################################
# Machine Learning sur les données enrichies après scraping
#############################################################
#Lecture des données suite à scraping ############
dfQPPS8 = pd.read_csv("dfQPPS7.csv")
dfQPPS8.info(verbose=True) # 12194 enregistrements.
dfQPPS8.reset_index(inplace=True, drop=True)
#Variables explicatives
X = dfQPPS8[['isHttps', 'level',
'lenWebSite', 'lenTokensWebSite', 'lenTokensQueryInWebSiteFrequency', 'sumTFIDFWebSiteFrequency',
'lenPath', 'lenTokensPath', 'lenTokensQueryInPathFrequency' , 'sumTFIDFPathFrequency',
'lenTitle', 'lenTokensTitle', 'lenTokensQueryInTitleFrequency', 'sumTFIDFTitleFrequency',
'lenDescription', 'lenTokensDescription', 'lenTokensQueryInDescriptionFrequency', 'sumTFIDFDescriptionFrequency',
'lenH1', 'lenTokensH1', 'lenTokensQueryInH1Frequency' , 'sumTFIDFH1Frequency',
'lenH2', 'lenTokensH2', 'lenTokensQueryInH2Frequency' , 'sumTFIDFH2Frequency',
'lenH3', 'lenTokensH3', 'lenTokensQueryInH3Frequency' , 'sumTFIDFH3Frequency',
'lenH4', 'lenTokensH4','lenTokensQueryInH4Frequency', 'sumTFIDFH4Frequency',
'lenH5', 'lenTokensH5', 'lenTokensQueryInH5Frequency', 'sumTFIDFH5Frequency',
'lenH6', 'lenTokensH6', 'lenTokensQueryInH6Frequency', 'sumTFIDFH6Frequency',
'lenB', 'lenTokensB', 'lenTokensQueryInBFrequency', 'sumTFIDFBFrequency',
'lenEM', 'lenTokensEM', 'lenTokensQueryInEMFrequency', 'sumTFIDFEMFrequency',
'lenStrong', 'lenTokensStrong', 'lenTokensQueryInStrongFrequency', 'sumTFIDFStrongFrequency',
'lenBody', 'lenTokensBody', 'lenTokensQueryInBodyFrequency', 'sumTFIDFBodyFrequency',
'elapsedTime', 'nbrInternalLinks', 'nbrExternalLinks' ]] #variables explicatives
X.info()
y = dfQPPS8['group']
#on va scaler
scaler = StandardScaler()
scaler.fit(X)
X_Scaled = pd.DataFrame(scaler.transform(X.values), columns=X.columns, index=X.index)
X_Scaled.info()
#on choisit random_state = 42 en hommage à La grande question sur la vie, l'univers et le reste
#dans "Le Guide du voyageur galactique" par Douglas Adams. Ceci afin d'avoir le même split
#tout au long de notre étude.
X_train, X_test, y_train, y_test = train_test_split(X_Scaled,y, random_state=42)
Méthode des K plus proches voisins
On va rechercher le « meilleur » K en le faisant varier. le choix se fait au meilleur test score.
######################################################
# MODELE KNN
######################################################
#pour KNN recherche du nombre de voisins optimal
nMax=20 #nombre max de voisins
myTrainScore = np.zeros(shape=nMax)
myTestScore = np.zeros(shape=nMax)
myTrainTestScore = np.zeros(shape=nMax)
for n in range(1,nMax) :
print("n_neighbors:"+str(n))
knn = KNeighborsClassifier(n_neighbors=n)
knn.fit(X_train, y_train)
myTrainScore[n]=knn.score(X_train,y_train)
print("Training set score: {:.3f}".format(knn.score(X_train,y_train))) #
myTestScore[n]=knn.score(X_test,y_test)
print("Test set score: {:.4f}".format(knn.score(X_test,y_test))) #
#Graphique train score vs test score
sns.set() #paramètres esthétiques ressemble à ggplot par défaut.
fig, ax = plt.subplots() #un seul plot
sns.lineplot(x=np.arange(1,nMax), y=myTrainScore[1:nMax])
sns.lineplot(x=np.arange(1,nMax), y=myTestScore[1:nMax], color='red')
fig.suptitle("Les scores diminuent avec le nombre de voisins.", fontsize=14, fontweight='bold')
ax.set(xlabel='n neighbors', ylabel='Train (bleu) / Test (rouge) / F1 (jaune)',
title="")
fig.text(.2,-.06,"Classification Knn - Univers de Concurrence - Position dans 2 groupes \n vs variables construites + variables pages en fonction des n voisins",
fontsize=9)
#plt.show()
fig.savefig("QPPS6-KNN-Classifier-2goups.png", bbox_inches="tight", dpi=600)
#on choist le meilleur test score
#à vérifier toutefois en regardant la courbe.
indices = np.where(myTestScore == np.amax(myTestScore))
n_neighbor = indices[0][0]
n_neighbor
knn = KNeighborsClassifier(n_neighbors=n_neighbor)
knn.fit(X_train, y_train)
print("N neighbor="+str(n_neighbor))
print("Training set score: {:.3f}".format(knn.score(X_train,y_train))) #
print("Test set score: {:.4f}".format(knn.score(X_test,y_test)))
#Test Score retenu pour knn : 0.7553 avec 2 voisins
#légèrement meilleur que précédemment avec moins de variables : 0,7368
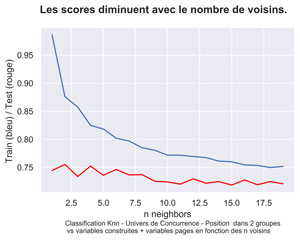
Le meilleur Test score est pour 2 voisins
N neighbor=2
Training set score: 0.876
Test set score: 0.7553
Régression Logistique
Voyons ce que l’on obtient avec la régression logistique en faisant varier le paramètre de régularisation C.
###############################################################################
#Classification linéaire 1 : Régression Logistique
#on faire varier C : inverse of regularization strength; must be a positive float.
#Like in support vector machines, smaller values specify stronger regularization.
myC=1
print("Regression Logistique myC="+str(myC))
logreg = LogisticRegression(C=myC, solver='lbfgs', max_iter=1000).fit(X_train,y_train)
print("Training set score: {:.3f}".format(logreg.score(X_train,y_train)))
print("Test set score: {:.3f}".format(logreg.score(X_test,y_test)))
#le test score 0.700 est moins bon que pour knn 0.7553
myC=100
print("Regression Logistique myC="+str(myC))
logreg100 = LogisticRegression(C=myC, solver='lbfgs', max_iter=1000).fit(X_train,y_train)
print("Training set score: {:.3f}".format(logreg100.score(X_train,y_train)))
print("Test set score: {:.3f}".format(logreg100.score(X_test,y_test)))
#le test score 0.700 est moins bon que pour knn 0.7553 .
myC=0.01
print("Regression Logistique myC="+str(myC))
logreg001 = LogisticRegression(C=myC, solver='lbfgs',max_iter=1000).fit(X_train,y_train)
print("Training set score: {:.3f}".format(logreg001.score(X_train,y_train)))
print("Test set score: {:.3f}".format(logreg001.score(X_test,y_test)))
#le test score 0.699 est moins bon que pour knn 0.7553 .et que pour C=1 ou C=100
myC=1000
print("Regression Logistique myC="+str(myC))
logreg1000 = LogisticRegression(C=myC, solver='lbfgs', max_iter=1000).fit(X_train,y_train)
print("Training set score: {:.3f}".format(logreg1000.score(X_train,y_train)))
print("Test set score: {:.3f}".format(logreg1000.score(X_test,y_test)))
#pareil le test score 0.700 est moins bon que pour knn 0.7553 .
Les résultats sont moins bon que pour KNN. Notre meilleur test score est obtenu avec C = 1, 100 ou 100 :
Regression Logistique myC=1
Training set score: 0.697
Test set score: 0.700
Machine à vecteurs de support linéaire
############################################################
#Classification linéaire 2 : machine à vecteurs de support linéaire (linear SVC).
LinSVC = LinearSVC(max_iter=100000).fit(X_train,y_train)
print("Training set score: {:.3f}".format(LinSVC.score(X_train,y_train)))
print("Test set score: {:.3f}".format(LinSVC.score(X_test,y_test)))
y_pred=LinSVC .predict(X_Scaled)
print("F1-Score : {:.4f}".format(f1_score(y, y_pred, average ='weighted')))
Ce modèle ne fait pas mieux. En plus il faut un nombre d’itérations importantes pour que le modèle converge. Ici même à 100.000 itérations on a une erreur.
Training set score: 0.693
Test set score: 0.685
Régularisation Ridge
On fera varier le paramètre alpha : 1, 10 et 0,1.
############################################################
#Ridge
#régression ridge avec la valeur par défaut du paramètre de contrôle
#alpha=1,
ridge = Ridge().fit(X_train,y_train)
print("Training set score: {:.2f}".format(ridge.score(X_train,y_train)))
print("Test set score: {:.2f}".format(ridge.score(X_test,y_test)))
#valeurs étranges
#Training set score: 0.08
#Test set score: 0.05
#Autres valeurs pour Ridge
ridge10 = Ridge(alpha=10).fit(X_train,y_train)
print("Training set score: {:.2f}".format(ridge10.score(X_train,y_train)))
print("Test set score: {:.2f}".format(ridge10.score(X_test,y_test)))
#valeurs étranges
#Training set score: 0.08
#Test set score: 0.06
ridge01 = Ridge(alpha=0.1).fit(X_train,y_train)
print("Training set score: {:.2f}".format(ridge01.score(X_train,y_train)))
print("Test set score: {:.2f}".format(ridge01.score(X_test,y_test)))
#valeurs étranges
#Training set score: 0.08
#Test set score: 0.05
Le modèle Ridge produit des valeurs aberrantes.
Régularisation Lasso
on fait varier le paramètre alpha : 1, 0,01, 10, 0,0001
##############################################
#Lasso
#Valeurs par défaut alpha=1
lasso = Lasso().fit(X_train,y_train)
print("Training set score: {:.2f}".format(lasso.score(X_train,y_train)))
print("Test set score: {:.2f}".format(lasso.score(X_test,y_test)))
print("Number of features used: {}".format(np.sum(lasso.coef_ != 0)))
#Valeurs étranges
#Training set score: 0.00
#Test set score: -0.00
#Number of features used: 0
#Lasso autres valeurs
lasso001 = Lasso(alpha=0.01,max_iter=100000).fit(X_train,y_train)
print("Training set score: {:.2f}".format(lasso001.score(X_train,y_train)))
print("Test set score: {:.2f}".format(lasso001.score(X_test,y_test)))
print("Number of features used: {}".format(np.sum(lasso001.coef_ != 0)))
#Valeurs étranges
#Training set score: 0.07
#Test set score: 0.07
#Number of features used: 18
lasso10 = Lasso(alpha=10,max_iter=100000).fit(X_train,y_train)
print("Training set score: {:.2f}".format(lasso10.score(X_train,y_train)))
print("Test set score: {:.2f}".format(lasso10.score(X_test,y_test)))
print("Number of features used: {}".format(np.sum(lasso10.coef_ != 0)))
#Valeurs étranges
#Training set score: 0.00
#Test set score: -0.00
#Number of features used: 0
lasso00001 = Lasso(alpha=0.0001,max_iter=100000).fit(X_train,y_train)
print("Training set score: {:.2f}".format(lasso00001.score(X_train,y_train)))
print("Test set score: {:.2f}".format(lasso00001.score(X_test,y_test)))
print("Number of features used: {}".format(np.sum(lasso00001.coef_ != 0)))
#Valeurs étranges
#Training set score: 0.08
#Test set score: 0.06
#Number of features used: 57
Lasso donne aussi des valeurs étranges.
Régularisation ElasticNet
On va faire varier les paramètre alpha et l1_ratio
##############################################
#régression elastic-net
#avec les valeurs par défaut des paramètres de contrôle.
baseElasticNet = ElasticNet().fit(X_train,y_train)
print("Training set score: {:.2f}".format(baseElasticNet.score(X_train,y_train)))
print("Test set score: {:.2f}".format(baseElasticNet.score(X_test,y_test)))
print("Number of features used: {}".format(np.sum(baseElasticNet.coef_ != 0)))
#Valeurs étranges
#Training set score: 0.00
#Test set score: -0.00
#Number of features used: 0
#ElasticNet avec plusieurs valeurs pour alpha et l1_ratio
import itertools #pour itérer sur 2 variables.
a=[0.0001, 0.001, 0.01, 0.1, 0.2, 0.3]
l=[0.0001, 0.01, 0.1, 0.5, 1]
myENTestScore = []
for myAlpha, myL1 in itertools.product(a,l) :
myElasticNet = ElasticNet(alpha=myAlpha, l1_ratio=myL1 ).fit(X_train,y_train)
print("Alpha: {:.6f}".format(myAlpha))
print("L1 Ratio: {:.6f}".format(myL1))
print("Training set score: {:.2f}".format(myElasticNet.score(X_train,y_train)))
print("Test set score: {:.2f}".format(myElasticNet.score(X_test,y_test)))
print("Number of features used: {}".format(np.sum(myElasticNet.coef_ != 0)))
myENTestScore.append(myElasticNet.score(X_test,y_test))
#le max des Test Score pour ElasticNet
max( myENTestScore)
#le meilleur test score 0.07332222123115184 valeur aberrantes
Le modèle ElasticNet donne aussi des valeurs aberrantes.
Graphique Importance des variables.
On va faire le graphique pour la régression logistique avec C=1 (standard) qui a eu le meilleur test Score des modèles linéaires :
#######################################################################
# Affichage de l'importance des variables on prend logreg qui
# est le "meilleur"
#######################################################################
signed_feature_importance = logreg.coef_[0] #pour afficher le sens
feature_importance = abs(logreg.coef_[0]) #pous classer par importance
#feature_importance = 100.0 * (feature_importance / feature_importance.max())
sorted_idx = np.argsort(feature_importance)
pos = np.arange(sorted_idx.shape[0]) + .5
sns.set() #paramètres esthétiques ressemble à ggplot par défaut.
fig, ax = plt.subplots() #un seul plot
fig.set_figheight(15)
ax.barh(pos, signed_feature_importance[sorted_idx], align='center')
ax.set_yticks(pos)
ax.set_yticklabels(np.array(X.columns)[sorted_idx], fontsize=8)
#fig.suptitle("aaa \n bbb ", fontsize=10)
ax.set(xlabel='Importance Relative des variables\nRégression Logistique C=1 - Univers de concurrence - Importance des variables',
title="La taille du Body en caractères et en nombre de mots sont les 2 facteurs importants \n toutefois dans un sens différent !")
fig.savefig("QPPS6-logreg1000-Importance-Variables-2goups.png", bbox_inches="tight", dpi=600)
##############################################################
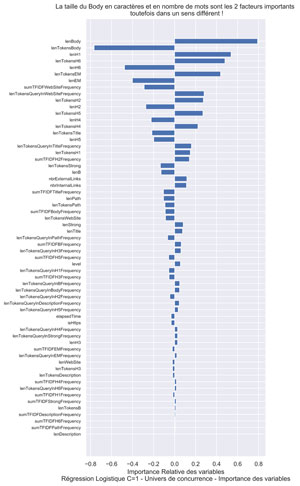
Le fait que la longueur en caractères et en nombre de mots du corps influencent de façon contraire le modèle nous montre ici simplement que la longueur des mots est importante.
Il serait judicieux à l’avenir d’enlever les « stopwords » i.e. les petits mots non significatifs : le, la, les, des, au, mes … de nos variables.
Modèle XGBoost
Calculons XGBoost avec les paramètres par défaut.
#########################################################################
# XGBOOST
##########################################################################
#xgboost avec parametres standards par défaut
myXGBoost = XGBClassifier().fit(X_train,y_train)
print("Training set score: {:.3f}".format(myXGBoost.score(X_train,y_train)))
print("Test set score: {:.3f}".format(myXGBoost.score(X_test,y_test)))
#pour info : parametres par défaut
myXGBoost.get_xgb_params()
##########################################################################
# MERCI pour votre attention !
##########################################################################
#on reste dans l'IDE
#if __name__ == '__main__':
# main()
Les scores donnent les valeurs suivantes :
Training set score: 0.755
Test set score: 0.734
Si le Test Score pour XGBoost est moins bon que celui de KNN (0,734 vs 0.7553) , il est bien meilleur que le meilleur score pour la régression logistique (0,700). Ceci est encourageant.
Dans l’article suivant, nous verrons que nous pourrons améliorer grandement ce score en optimisant les hyper-paramètres d’XGBoost au moyen d’un algorithme génétique.
A bientôt,
Pierre